はじめに

マサト先生
やあ、こんにちは!今日は単回帰分析の応用問題を前回作ったプログラムを使って解決しよう。

ヒロト
はい、よろしくお願いします。

マサト先生
問題は、次の通りだ。
問題
あなたはある町で不動産業を営んでいる。
現在所有している物件の家賃は下の表のとおりとなっている。
| \(m^{2}\) | 20 | 30 | 40 | 50 | 60 |
| 家賃 | 60000 | 85000 | 115000 | 150000 | 180000 |
さて、新しく手に入った広さ \(45m^{2}\) の部屋の家賃を最も適切に決めたい。いくらにすればいいか?

ヒロト
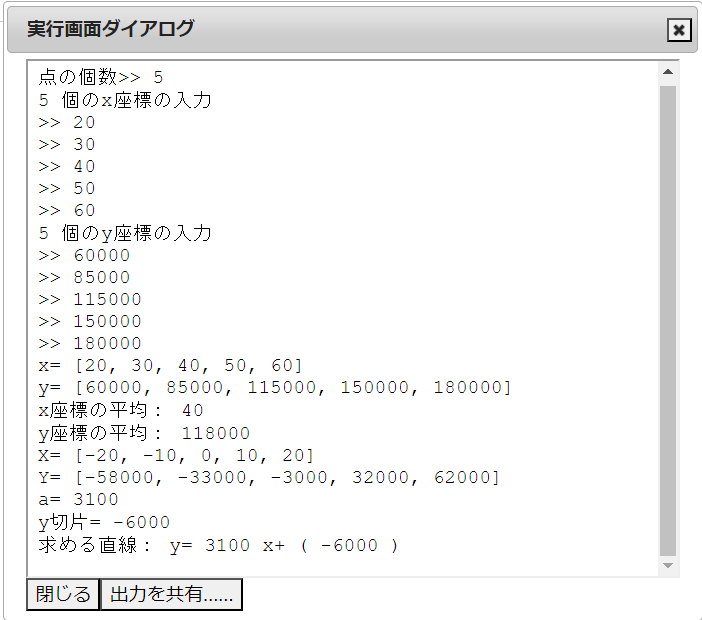
なるほど、こういう時に単回帰分析が役に立つのですね!では前回作成したプログラム『file57』を呼び出して求めてみたいと思います。リストxには20,30,40,50,60を代入し、リストyには60000,85000,115000,150000,180000を代入すればいいはずです。実際入力して実行された結果が下の画面です。
解答

ヒロト
プログラムによると、与えられた5個の点に最もフィットする直線は
$$y=3100x+(-6000)$$
となります。ということは、広さ \(45m^{2}\) の部屋の家賃を最も適切に決めるには、この直線の式に \(x=45\) を代入すればいいので、求める家賃は、
$$y=3100 \times 45 – 6500=139500-6500=133000(円)$$
となります。

マサト先生
完璧だ!この問題のように『単回帰分析』は既に存在しているデータを基にして、未知のデータを適切に決定したいときに役に立つのだ!

ヒロト
応用の幅がとても広そうですね!
場合によっては未来の予測とかも出来そうですね!

マサト先生
その通りだ。ぜひいろいろな問題を自分で設定して考えてみて欲しい。土台となるプログラムは既にできているのだから容易に調べられるはずだ。

ヒロト
はい!

マサト先生
では、今日はここまでにしよう。お疲れさん。

ヒロト
はい!ありがとうございました!





コメント