前回の復習

やあ、こんにちは。今日は前回学んだ『単回帰分析』の数学的な手続きをプログラムで書くことが目的だ。しっかり復習してきたかな?

はい、しっかり復習してきました。よろしくお願いします。

うむ。まずは前回学んだことを復習してみよう。
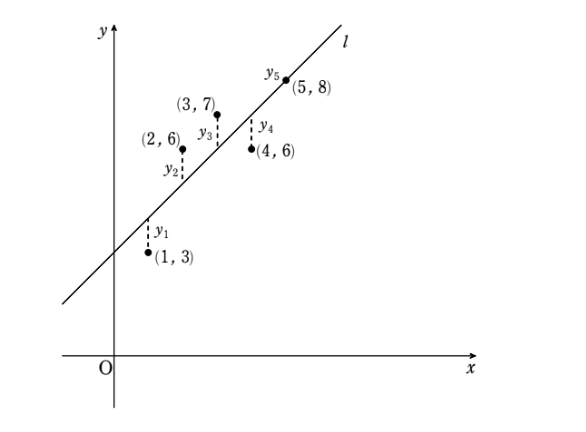
まずは適当な5個の点の座標が与えられたとしよう。次に何をしたかというと、\(x\) の平均 \(\bar{x}\) と \(y\) の平均 \(\bar{y}\) を求め、それぞれ\(x\) 座標と\(y\) 座標から引いて、新しい5個の座標を求めるのだった。この作業を座標の中心化と言うのであった。さて、次はどうするのだったかな?

はい、新しい座標を求めた後は、直線 \(y=ax\) と新しい点の \(y\) 座標との『差の2乗和』を求めます。そして、その2乗和を最小にするような傾き \(a\) を求めるのでした。前回の計算によると2乗和は『2次関数』になったので平方完成することによって求めることができました!

うむ、しっかり復習してきているな!感心感心。
さて、今言ったような流れを一つ一つプログラムに書き換えて行ってもよいが、もう少しコンパクトにまとめられないかを考えよう。そのためには、一般的な数学の議論を通して調べるのがよくやる方法なのだ。以下、一緒にやってみよう。

はい、お願いします。
一般的な議論の大切さと微分の威力

さて、与えられた \(n\) 個の座標を一般に \((x_i\ ,\ y_i)\ \ (1 \le i \le n)\) としよう。そして、中心化された座標をそれぞれ \(X_i=x_i-\bar{x}\ ,\ Y_i=y_i-\bar{y}\) と書くことにする。この中心化された \(n\) 個の点 \((X_i\ ,\ Y_i)\ \ (1 \le i \le n)\) に最もフィットする直線 \(Y=aX\) を求めることを考えよう。ここまでいいかな?

はい、大丈夫です。この後『差の2乗和』をとって、出てきた2次関数を平方完成して最もフィットする傾き \(a\) を求めたのでした。

うむ、前回はそのようにしたな。今回は平方完成ではなく、あえて『微分』使いたいと思う。微分も関数の最小値求めるための強力な道具だったことを思い出してほしい。

確かに微分は『導関数=0』、つまり 『 \(f^{\prime}(x)=0\) 』 を解くことによって最小値を与える \(x\) が求められました!

うむ、ではここまでを数式を用いて見ていこう。下に板書をまとめたからじっくり読んでいってくれ。
中心化された \(n\) 個の点 \((X_i\ ,\ Y_i)\ \ (1 \le i \le n)\) の \(y\) 座標と直線 \(y=ax\) と『差の2乗和』を \(f(a)\) とおくと
$$f(a)=\sum_{i=1}^{n}(Y_i-aX_i)^{2}$$
これを、\(a\) で微分すると微分の線形性と合成関数の微分法より、
$$f^{\prime}(a)=\sum_{i=1}^{n}\{(Y_i-aX_i)^{2}\}^{\prime}$$
$$=\sum_{i=1}^{n}2(Y_i-aX_i)\cdot(-X_i)$$
$$=2\sum_{i=1}^{n}(aX_i^{2}-X_iY_i)$$
$$=2a\sum_{i=1}^{n}X_i^{2}-2\sum_{i=1}^{n}X_iY_i$$
となるので、\(f^{\prime}(a)=0\) を \(a\) について解いて、
$$a=\frac{\sum_{i=1}^{n}X_iY_i}{\sum_{i=1}^{n}X_i^{2}}$$
を得る。

どうだ?微分を用いることによって、シグマ記号を外すことなく求めたかった \(a\) の表示が得られただろう?平方完成を使う場合は、シグマ記号を計算して外してから更に2乗を計算して、同類項をまとめなくてはならないという手間が生じたことを思い出してほしい。

おお、凄い!微分の威力が改めて分かりました。
結局、
$$a=\frac{\sum_{i=1}^{n}X_iY_i}{\sum_{i=1}^{n}X_i^{2}}$$
を計算してくれるプログラムを書いて、最もフィットする傾きを求めればいいということですね!そして、元の位置に平行移動すると、
$$y=a(x-\bar{x})+\bar{y}=ax+(\bar{y}-a\bar{x})$$
となる!つまり、\(y\) 切片は \(\bar{y}-a\bar{x}\) を計算して得られるということです。

よし、ではそろそろプログラムを書いてもらおうかな。準備はいいかな?

はい、今回は『file57』から書いていきます。
ではしばらく時間をください。
オリジナルの単回帰分析のプログラム
約1時間後

ふう、やっとできました!
とても長いプログラムになりましたが多分これでいいと思います。
まずは下の前半部分について説明します。
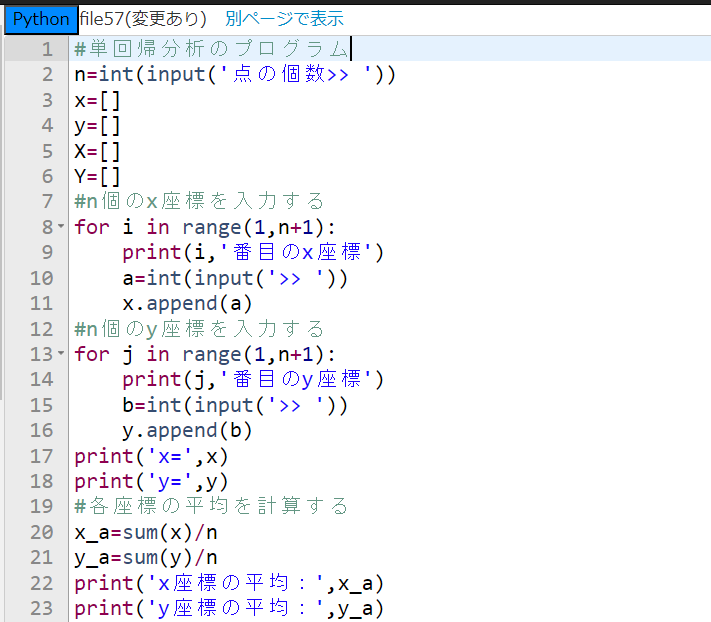
2行目では点の個数nをキーボードから入力するようにしました。
3行目から6行目までは、後で使う空のリストを用意しています。8行目から11行目までのfor文では空のリストxにn個のx座標をキーボードから入力できるようにしています。13行目から16行目までのfor文も同様に空のリストyにn個のy座標をキーボードから入力できます。17・18行目でちゃんと入力されたか表示します。20から23行目では、x座標とy座標の平均を計算しそれぞれx_aとy_aに代入して表示するようにしました。ここまでが前半部分です。

うむ、途中に『#』で説明文を付けているのが分かりやすくていいな!続けてくれ。

はい、では続いて下の後半部分について説明します。
25~30行目では、for文を用いて各座標から各平均を引いて、それぞれ空のリストのXとYに追加しています。これは点の中心化をしたということです。32~38行目では、一般論から求めた傾きの公式:
$$a=\frac{\sum_{i=1}^{n}X_iY_i}{\sum_{i=1}^{n}X_i^{2}}$$
を計算するプログラムです。最後に元の位置に平行移動したときのy切片 \(\bar{y}-a\bar{x}\) を計算して、完成した直線の式を表示して終わりとなります!


このプログラムを実行した結果が下の画面になります。
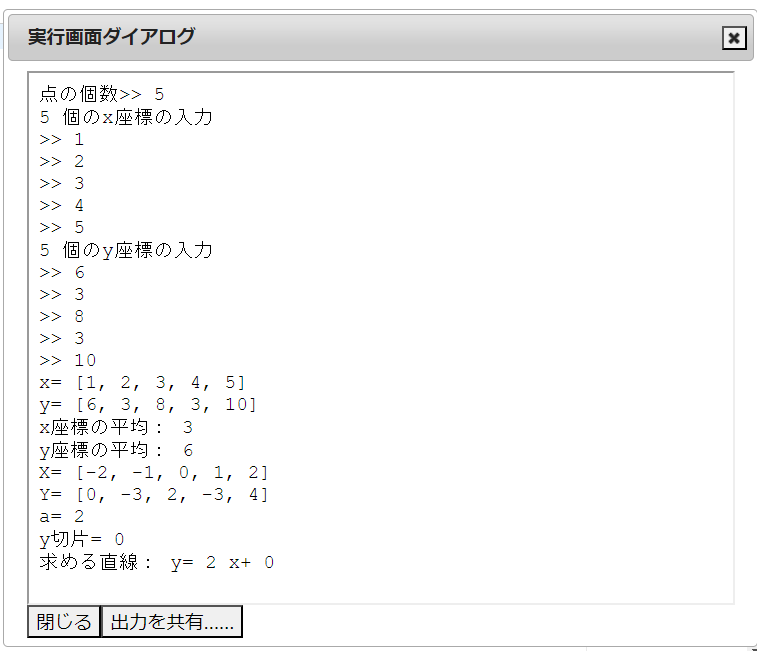

頑張ったな!最初に入力する点の個数を自由に指定できるところや、リストをうまく用いて平均や傾きを求めているところに工夫を感じたぞ!次回は単回帰分析の応用問題を出すから、今回作ったプログラムを使って解いてみよう!では今日もお疲れさん。

はい、ありがとうございました!



コメント