微分とは何か?

では、今回から微分の基礎について学んでいこう。

はい、よろしくお願いします!

さて、はじめにヒロトに聞きたいことがある。
『微分って何だ?』

うっ!いきなり核心を突く質問ですね。
うーん、どういえばいいのかな?
与えられた関数を微分はできるんだけど、、、。

うむ、計算できることも大切だが、ここで聞いているのは、数学的な厳密な定義ではなくて、微分に対して自分が持っているイメージだ。

えーと、ちょっと一言では言えないくらい奥が深いと思います。

うむ、うまくかわしたな。
微分って何?に対する俺の答えはこうだ!
『瞬間の速さの計算法!』

瞬間の速さですか?
速さっていうと小学校で習ったあの、『道のり÷時間』のやつですか?

いや、そのやり方で求めた速さを正確には『平均の速さ』と言うのだ。
ここで言う『瞬間の速さ』とは別物だ。

二つの速さはどう違うんですか?
平均の速さ

いい質問だ!具体例で説明しよう。
自宅から、どこでもいいがドライブに行ったことを想像してみてくれ。
例えば自宅から \(100㎞\) 離れている温泉まで行くのに\(2\) 時間かかったとしよう。
このとき、車の速さはどうなる?

えーと、普通に『道のり÷時間』をして、
\(100\div2=50\) つまり、時速 \(50km\) です。

そうなるな。しかしだ、少し想像してみてくれ。
車に乗って温泉に行くときずっと時速 \(50km\) で走っていたのかい?
信号もあるだろうし、途中どこかで休憩するかもしれないだろう?

うん、確かに。信号で止まったら速さは \(0\) になるし、高速とか使ったら、時速 \(50km\) より早く走ります。

すると、今求めた時速 \(50km\) というのはいったい何を意味するのか?

それは、途中過程は考えずにとにかく一定の時速 \(50km\) で走り続けたら、
2時間で温泉につくということを意味すると思います。あっ!これって平均だ!

ふふ、気づいたみたいだな。そう、つまりそういう事なんだ。
途中信号で止まったり、高速に乗って走ったりしたとしても、トータルで2時間かかったということは、これらの速さの平均を取ると、時速 \(50km\) だということだ。これが、『道のり÷時間』で求めた速さを、平均の速さという理由だ。下の図を見ればイメージしやすいだろう。
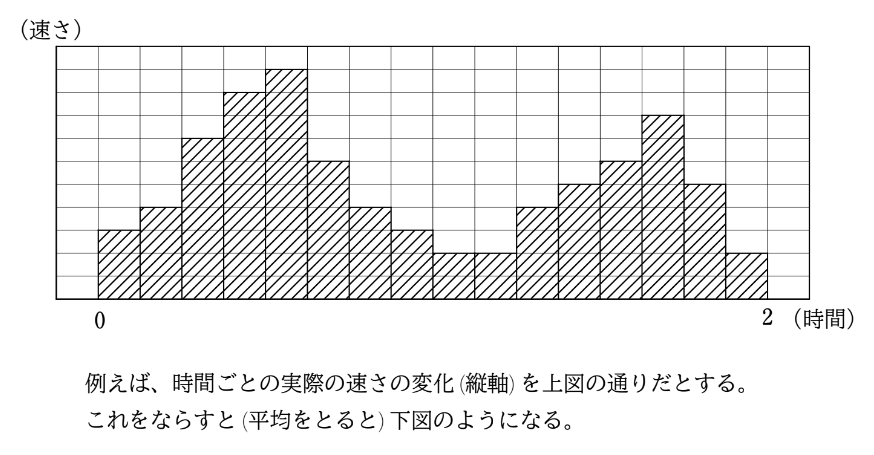
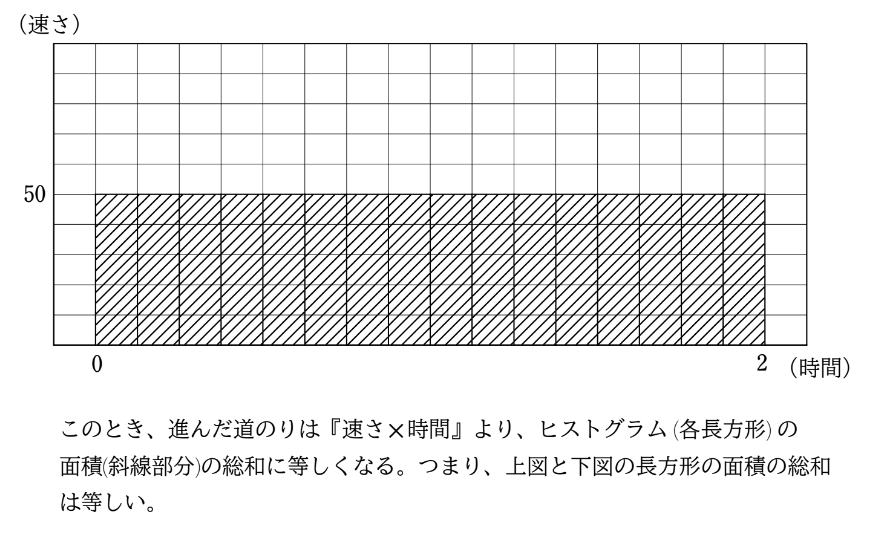

はい、とても納得しました。『道のり÷時間』は確かに平均の速さでした。

瞬間の速さ

では次に『瞬間の速さ』について説明しよう。
これは読んで字のごとくってやつだ。
ヒロトは車に乗っているとき、スピードメータ-を見たことあるだろう?
今車が何キロ出ているか教えてくれるメーターだ。

はい、もちろんです。
特に高速に乗っているときに、今何キロ出ているんだろう?って興味が湧くときがあります。今何キロって・・・、あっ!これって瞬間の速さだ!

ふふふ、また気づいたようだな。そういうことだ。
瞬間の速さとは、まさにスピードメーターに表示されている、
今この瞬間の速さのことだ。
これで、『平均の速さ』と『瞬間の速さ』の違いが分かったろう?

はい、分かりました!
平均の速さは『道のり÷時間』をやれば簡単に求められますが、
瞬間の速さを求める方法はあるのですか?

すでに言ったとおりだ。
瞬間の速さを求める計算法が微分だってな。

そういえば言ってましたね(笑)

瞬間の速さの計算法
グラフの導入

さて、問題がはっきりしたところで、いよいよ微分の核心へと歩を進めたいと思う。
視覚的に考えるためにグラフを描いて説明しよう。横軸を時間 \(x\)、
縦軸を距離 \(y\) としたおなじみの座標を使おう。車の時間と距離の関係を表したグラフは \(y=f(x)=25x^{2}\) として単純化しているぞ。
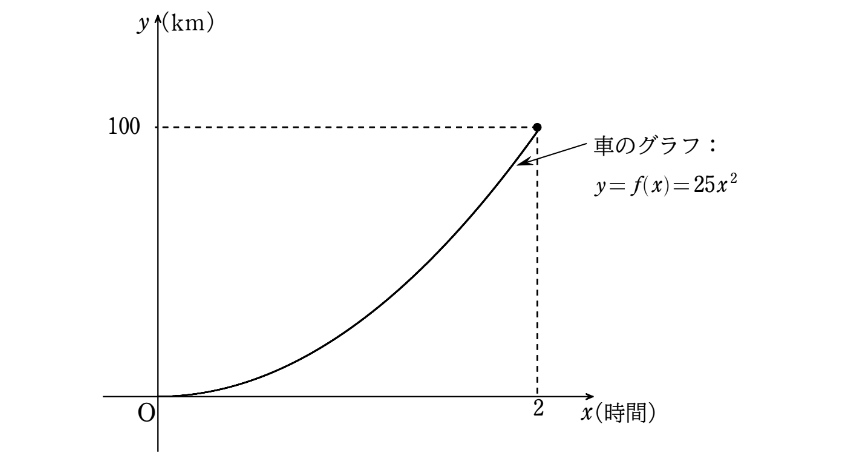

これは、車の速度がだんだんと上がっているという状況ですね。
グラフの世界における平均の速さ

ああ、ちょっと非現実的な状況だけど、考えやすくするための処置だと思ってくれ。
さて、先ほど自宅から温泉までの平均の速さを \(100\div2=50\) と求めたが、
これはこのグラフの世界では何を表しているか分かるかい?

グラフの世界で何を表すのか、ですか?
ええと、全くわかりません。

中1の頃に習う1次関数を思い出してほしい。
1次関数のグラフは直線だったな。そして、直線には傾きというものがあっただろう?傾きの定義を思い出してごらん。

はい、確か傾きの定義は、\(\frac{\Delta y}{\Delta x}\) だったと思います。
ここで、\(\Delta x\) は \(x\) の増加量を意味する記号で、デルタエックスと読みます。
\(\Delta y\) についても同様です。

完璧だ!ということは、平均の速さ \(\frac{100}{2}\) は、グラフ的に何を表しているかもう分かるのではないか?

ああ、そうか!\(x\) の増加量を2、\(y\) の増加量を100と見れば、
これは正に、傾きの定義そのものですね。
なので、原点と点 \((2 , 100)\) を結ぶ直線の傾きを表しているのですね!

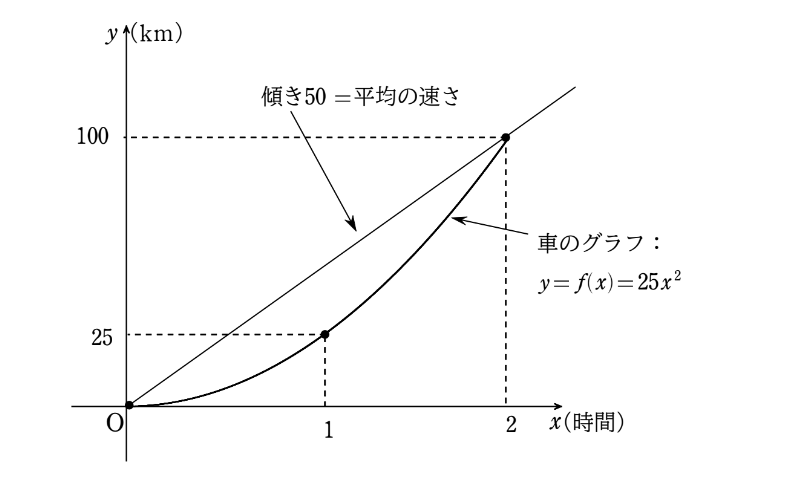
その通り!横軸が時間、縦軸が道のりのグラフにおいては、
平均の速さは、『2点を結ぶ直線の傾き』を表すことを忘れずにいてくれ。
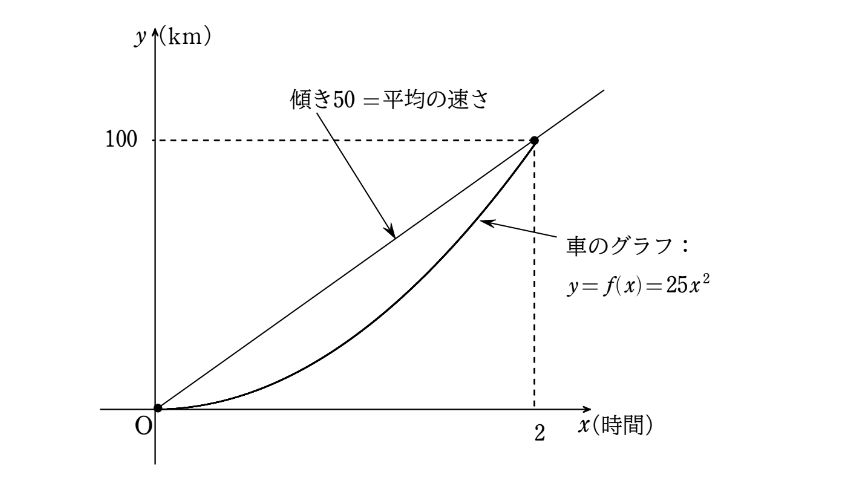

なるほど、平均速さはグラフ的には2点をむすぶ直線の傾きを表しているのですね!よく分かりました!
瞬間の速さの計算法

では、次に瞬間の速さのついて考えて行こう。
とりあえず、 \(x=1\) における瞬間の速さを実際に求めることから始めよう。
さて、\(x=1\) のとき \(y=25\) だから、車は自宅からちょうど \(25km\) 進んだ地点にいることになるな。 求めるのはその地点に達した瞬間のスピードメーターの値だ。

いったいどうやって計算するんだろう?
だって、 \(25km\) の地点に達した瞬間の速さって言われても、瞬間ってどういうことだろう?

うむ、とても自然な感覚だ。それでいいんだ。
もう少し具体的に考えてみよう。まず、1時間10秒後に車はどれくらい進んでいるか計算機を使ってもいいから計算してみてくれないか?

はい、それならできそうです。\(y=f(x)=25x^{2}\) であり、10秒を時間に直すと、\(\frac{1}{360}\) 時間なので、\(x=1+\frac{1}{360}=\frac{361}{360}\) を代入すればいいですね!計算機を使って、\(25\times(\frac{361}{360})^{2}=\frac{3258025}{129600}=25.139\cdots\) となります。計算機使えば楽勝ですね!

うむ、それは当たり前だぞ。
すると、『1時間から1時間10秒までの平均の速さ』が計算できるだろう?

はい、計算機があるのでなんでも来いです。
平均の速さは普通に計算すればいいので、次のように計算できます。
$$\Delta x=\frac{361}{360}-1=\frac{1}{360}\ ,$$
$$\Delta y=25.139\cdots – 25=0.139\cdots\ ,$$
であるから、
$$\frac{\Delta y}{\Delta x}=\frac{0.139\cdots}{(\frac{1}{360})}=0.139\cdots \times 360 \approx 50.07$$

よし、いいぞ。今求めたその『\(50.07\)』が、
『1時間から1時間10秒までの平均の速さ』ということだな。
つまり、わずか10秒間における平均の速さだ。

はい、そうなりますね。先生、これと瞬間の速さは何の関係があるのですか?

今にわかるさ、フフフ。
さて、大変なのを承知でもう一度同様の計算をしてもらうぞ。
今度は、『1時間から、1時間1秒までの平均の速さ』を計算してみてくれ。

1時間から、1時間1秒までの平均の速さですか!
1秒は \(\frac{1}{3600}\) 時間だから同様に計算できそうだけど・・・こりゃ大変になるぞ!

ああ、かなり大変になるだろうな。ところで、中1のときに文字式をせっかく習ったんだから使ってみよう!つまり、\(h=\frac{1}{3600}\) とおいて計算すればいいんだよ。そうするほうがずっといいんだ。

はい、とりあえず言われた通りやってみます。
でも先生、なんで文字は \(h\) なんですか?

それは、もちろんヒロトの『\(h\)』に決まってるだろう!

ありがとうございます!
では、書きながらやってみます。
1秒を \(h\) 時間と表したことになるから・・・
$$1時間から、1時間1秒まで \longrightarrow 1時間から、1+h 時間まで、$$
とかけるので、
$$x の増加量は、\Delta x=(1+h)-1=h、$$
$$y の増加量は、\Delta y=25(1+h)^{2}-25=25(1+2h+h^{2})-25=50h+25h^{2}$$

よって、平均の速さは・・・
$$\frac{\Delta y}{\Delta x}=\frac{50h+25h^{2}}{h}=50+25h$$

となります。\(h=\frac{1}{3600}\) なので、これを代入すると・・・
$$25h+50=25 \times \frac{25}{3600}+50=0.006944\cdots +50 \approx 50.0069$$

はい、できました!
1時間から1時間1秒までの平均の速さは、\(50.0069\)です。
文字式で計算してから後で代入する方がずっと楽でした。

そうだろう?
さて、文字を使うことは、計算が楽になるのともう一つとても重要な役割があるのだ。
それは、一度 \(h\) を用いて計算してしまえば、あとは \(h\) に好きな数を代入すればよいということだ!

なるほど!つまり、最終的な計算結果である、\(50+25h\) の \(h\) に好きな数を代入すれば途中計算はしなくてよくなるのですね!

正にその通りだ!では、もう次の質問も怖くはないな?
『1時間から1時間0.1秒までの平均の速さ』はどうなる?

ええと、0.1秒は \(\frac{1}{36000}\) 時間だから、
\(50+25h\) に \(h=\frac{1}{36000}\) を代入して、
$$50+\frac{25}{36000}=50+0.0006944\cdots=50.0006944\cdots \approx 50.00069$$

・・・となります。

うむ!では、
『1時間から1時間0.01秒までの平均の速さ』はどうなる?

ノートに書いていたおかげで、もう計算しなくとも予想できるぞ!
1時間から1時間1秒までのとき、50.0069
1時間から1時間0.1秒までのとき、50.00069 になるということは、
1時間から1時間0.01秒までのときは、50.000069 になるに違いない!

そうだな、そのような推測はどんどんしてくれ!
そろそろいい頃合いだな。
ところで、ヒロトよ、今我々は何を求めようとしてるのだ?

ええと、たしか \(x=1\) のときの瞬間の速さです。
つまり、出発してからちょうど1時間後の速さでした。

そうだったな。そして、我々は上の計算で1時間からわずかに時間をずらして、その間の平均の速さを求めてきたのであった。さて、このわずかにずらす時間をもっともっと短い時間にしていくとどうなるだろうか?

ええと、普通に考えると、1時間からもっともっと短い時間進んだ時の平均の速さが求まります。その値は、実験からどうやら50に近づいていくようです。
1秒ずらしたときの平均速さ・・・50.0069、
0.1秒ずらしたときの平均速さ・・・50.00069、
0.01秒ずらすしたときの平均速さ・・・50.000069、
以下同様に、50.0000069、50.00000069、50.000000069・・・と続いていく。

うん、それは正しい予想だ!
1時間からずらす時間をどんどん短くしていくと、その時の平均の速さは『1時間後の瞬間の速さ』に近づいていく。『瞬間』というのは具体的な数として表せないから、上の計算のように限りなく0に近づけていく方法をとるしかないのだ。

なるほど、1時間後の瞬間の速さというのは、1時間からほんのわずかに進んだ間の平均の速さのことだったのですね!実験から得た予測によるとその値は \(50km/時\) に限りなく近づいていきます。これが1時間に達したときの瞬間の速さになるということですか?

その通りだ。今まさに我々は瞬間の速さの導出に成功したのだ!
そして、この計算法を数学的にコンパクトに表現したものが『微分』ということになるのだ。

瞬間の速さの計算法は、平均の速さの計算法が基になっているのですね!
グラフの世界における瞬間の速さ

ああ、その通りだ!では、最後の質問をしたいと思う。
瞬間の速さはグラフの世界では何を表しているのだろうか?

平均の速さは、ある2点を結ぶ直線の傾きを表していました。
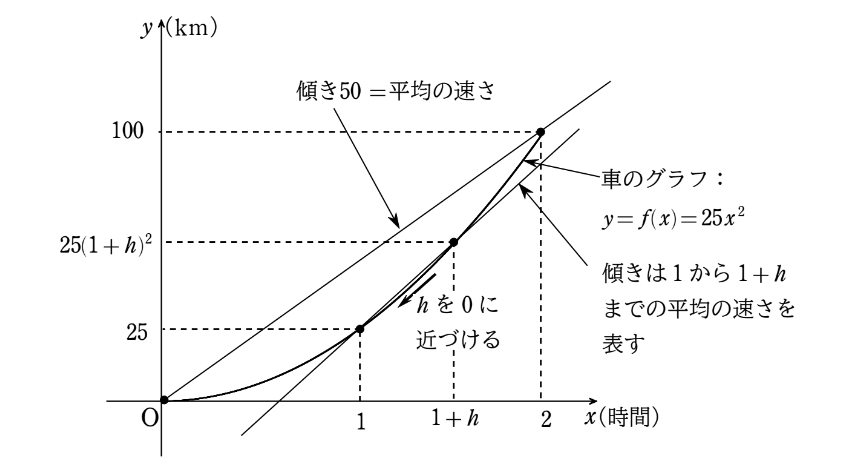
そして、瞬間の速さは、\(x=1\) から \(x=1+h\) までの平均の速さを、 \(h\) をどんどん0に近づけていくことで得られる平均の速さということなので、グラフの世界においては2点 \((1 , 25)\) と \((1+h , f(1+h))\) を結ぶ直線において、\(h\) が0に近づいていくときの直線の傾きを表します。なので、結局は点 \((1 , 25)\) を通る接線の傾きに一致することになりそうです。

ああ、その通りだ!
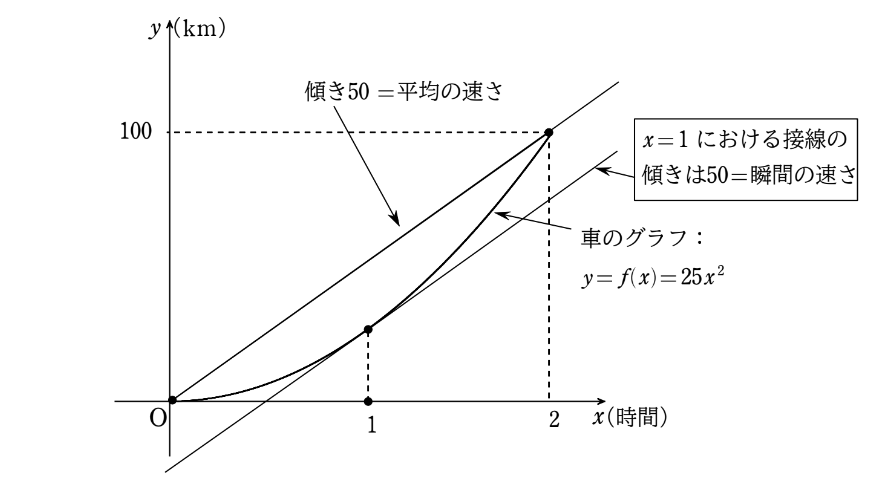
平均の速さは、ある2点間の傾き、
瞬間の速さは、ある1点における接線の傾きを表すということだ。
さて、第1回はここまでにしよう。
次回は数学的な微分の定義とその性質についてやろうと思う。
今日はお疲れさん。

はい、ありがとうございました!
ティーブレイク

万有引力の発見で有名な『アイザック・ニュートン』は、実は微分積分の創始者の一人である。物体の運動の研究をしていたニュートンは、詳しく分析するために自然と『瞬間の速さの計算法』の必要性に気づくようになった。そして、平均の速さを基にして上で紹介したように瞬間の速さを導出したのだろう。
ニュートンのすごいところは、それだけに留まらず、『極限』という概念を導入し、数学的に簡潔に表現して、それ自体をさらに詳しく研究し、様々な自然現象に応用したことである。その功績の一つとして天体への応用が挙げられる。
いくつかの単純な過程(ニュートンの運動の法則)を設けて、天体の運動を数学的に分析し、惑星が楕円軌道を描くことを始めて数学的に証明したりした。ここまで大体的に数学を自然に応用し、成功した例は他にない。
『必要は発明の母』というが、きっかけは運動をより詳しく調べるために必要となった『瞬間の速さの計算法』であった。それが、『微分』という数学的な概念に昇華し、今現在となっては様々な科学技術に応用され我々に恩恵を与えてくれているのだ。





コメント