第六回 解答
問題.16 解答
証明の前に
証明の前に、写像 \(f : A \longrightarrow B\) が線形写像であることの定義と、単射であることの定義を確認しておこう。これを知らないと絶対に解けないのだ。
まず、写像 \(f : A \longrightarrow B\) が次の性質を満たすとき \(f\) は線形であるという。
『任意の \(a、b \in \mathbb{R}\ (or\ \mathbb{C})\) と任意の \(x、y \in A\) に対して、
\(f(ax+by)=af(x)+bf(y)\)』、
線形写像の例として例えば、\(f(x)=ax (a は定数)\) という一次関数がある。これは、原点を通る直線(つまり『線形』だ!)というところから線形写像の名前が付いたと考えられる。
他には、行列を掛ける写像 \(f_A(\boldsymbol{x})=A\boldsymbol{x}\) や、関数から関数への写像としての微分、積分などがある!(つまり数学の重要な演算は、線形写像だと言えるな)
また、写像 \(f : A \longrightarrow B\) が次の性質を満たすとき \(f\) は単射であるという。
『 \(a、b \in A に対して、f(a)=f(b) \Longrightarrow a=b\) 』
これはいったい何事だ? と思うかもしれないが、意味してる内容はいたってシンプルであることは、『対偶』をとってみるとすぐにわかる。
(対偶)\(a \ne b \Longrightarrow f(a) \ne f(b)\)
さあ、これでどうだろう? 分かりやすくなったのではないだろうか?
対偶の意味してることはつまり、『異なる元は、異なる元に飛ぶ』ということだ。
これが単射の意味である! 対偶ともとの主張は同値であるのに、なぜ分かりやすい対偶の主張の方を定義としないのだろうか? それは、もとの定義の方が証明のときには使いやすいからだ。このことは、解答を見てもらえば納得すると思うので、早速解答に移ろう。
(1)の証明
(1) (証明)
(\(\Longrightarrow\)) \(f : A \longrightarrow B\) は単射であるとする。
\(Kerf\) の任意の元を \(x\) とすると定義より、\(f(x)=0_B \cdots ①\) である。
また、\(f(0_A)=f(0_A+0_A)=f(0_A)+f(0_A)\) (\(f\): 線形写像より) であるから、\(f(0_A)=0_B \cdots ②\)
①、②から、\(f(x)=f(0_A)\) がいえるが、仮定より \(f\) は単射であるから、\(x=0_A\) となる。
\(x\) は \(Kerf\) の任意の元だったので、\(Kerf=\{0_A\}\) が示された。
(\(\Longleftarrow\)) 逆に \(Kerf=\{0_A\}\) であるとする。今、\(a、b \in A\) に対して、\(f(a)=f(b)\) であるとすると、\(f\): 線形より、$$f(a)-f(b)=0_B$$$$\Leftrightarrow f(a-b)=0_B$$よって、定義より \(a-b \in Kerf = \{0_A\}\) がいえる。よって、\(a-b=0_A \Leftrightarrow a=b.\)
これで、\(f(a)=f(b) \Longrightarrow a=b\) であることが示された。
故に、\(f\) は単射である。 \(q.e.d.\)
\(f\) の線形性と単射性が絶妙な働きをしていることが、それぞれ青下線部、赤下線部から分かる。
・写像 \(f : A \longrightarrow B\) が次の性質を満たすとき \(f\) は線形であるという。
『任意の \(a、b \in \mathbb{C}\) と任意の \(x、y \in A\) に対して、\(f(ax+by)=af(x)+bf(y)\)』
・写像 \(f : A \longrightarrow B\) が次の性質を満たすとき \(f\) は単射であるという。
『 \(a、b \in A に対して、f(a)=f(b) \Longrightarrow a=b\) 』(対偶が分かりやすい!)
これで(1)の解答を終わるがいかがだっただろうか? 私自身もそうであったように、最初はよく理解ができなかったが、本問も含め様々な証明に繰り返し触れることによって、「ああ、また同じ方法でやっているな」とか、「ああ、これは仮定を使うための変形だったのか」など段々と分かるようになっていき、いつしか自分で当たり前のように書けるようになるのだ。一字一句写すことはことはやめて、肩の力を抜いて何度も触れることが大切だ! では(2)の解答へ移ろう。
(2)の証明
(2) 証明
証明の前に、写像 \(f : A \longrightarrow B\) が全射であることの定義を確認しておこう。これを知らないと絶対に解けないのだ。
写像 \(f : A \longrightarrow B\) が次の性質を満たすとき \(f\) は全射であるという。
『任意の \(b \in B\) に対して、ある \(a \in A\) が存在して、\(b=f(a)\)』、
※\(f\) が単射でありかつ全射であるとき、\(f\) は全単射であるという。
さて、全射の定義を見てちょっとピンとこないときは、具体例を作ってみるとよいだろう。
例えば、\(\mathbb{R}\) から\(\mathbb{R}\) への写像で、\(f(x)=2x+1\) は全射で、\(f(x)=x^{2}\) は全射ではない。
なぜなら、前者の \(f(x)=2x+1\) は任意の実数 \(b\) に対して、\(x=\frac{b-1}{2}\) をとれば、\(f(\frac{b-1}{2})=b\) となって、全射の定義を満たすからだ。
また、後者の \(f(x)=x^{2}\) は、例えば、実数 \(-1\) に対して、\(f(x)=-1\) を満たす \(x\) が存在しない。よって、全射の定義を満たさないから全射ではない。
どうだろうか? このように簡単に具体例を作ることができたならその定義は完璧に理解したと思っていいだろう。もういくつか自分で具体例を見つけてみてほしい。私も、もう二つずつ紹介しよう。
(全射であるもの) \(f(x)=x^{3}\)、\(f(x)=logx\)
(全射でないもの) \(f(x)=sinx\)、\(f(x)=e^{x}\)
では、(2)の解答に移ろう。
(2) 証明
\(g \circ f\) は全単射だとする。
\(f\) が単射であること:
\(a、b \in A\) に対して、\(f(a)=f(b)\) とすると、両辺に \(g\) を作用させて、$$g(f(a))=g(f(b)) \Longleftrightarrow (g \circ f)(a)=(g \circ f)(b) \cdots ①$$
仮定により、\(g \circ f\) は全単射とくに単射であるから、①より \(a=b\) を得る。
つまり、単射の定義である、$$ a , b \in Aに対して、 f(a)=f(b) \Longrightarrow a=b$$が示されたので \(f\) は単射である。
\(g\) が全射であること:
任意の \(c \in C\) をとる。
仮定より、\(g \circ f\) は全単射、とくに全射なので、ある \(a \in A\) が存在して、\((g \circ f)(a)=c \Longleftrightarrow g(f(a))=c\) が成り立つ。
ここで、\(b=f(a)\) とおくと、\(g(b)=c\) となって、\(g\) は全射となる。 \(q.e.d.\)
これで、(2)の解答もできた。
合成写像:\(g \circ f\) が全単射であるとき、右側の \(f\) は単射で、左側の \(g\) は全射になるということだ。これは、知識として覚えてしまうとよいだろう。
賢明な方なら、「では、\(f\) は全射、かつ \(g\) は単射にはならないのか?」と考えるかもしれない。答えは、いずれも成立しない。
それは、反例としての具体例が作れるからだ。
例えば、\(f(x)=2^{x}、g(x)=logx\) とおくと、\(g \circ f\) は全単射となるが、\(f\) は全射ではない。
・写像 \(f : A \longrightarrow B\) が次の性質を満たすとき \(f\) は全射であるという。
『任意の \(b \in B\) に対して、ある \(a \in A\) が存在して、\(b=f(a)\)』
・合成写像:\(g \circ f\) が全単射であるとき、右側の \(f\) は単射で、左側の \(g\) は全射になる
問題.17 解答
解答の前に、\(3 \times 3\) 行列 \(A\) によって定まる線形写像 \(f_A : \mathbb{R^{3}} \longrightarrow \mathbb{R^{3}}\) とは、$$f_A(\boldsymbol{x})=A\boldsymbol{x}$$によって定められた写像のことである。(つまり、行列 \(A\) を左から掛ける写像である)
この写像が単射なのか全射なのか調べる問題である。どうやって調べるのだろう?と思うかもしれないが、このタイプの問題は、解き方が決まっている。
行列 \(A\) が正方行列のとき
行列 \(A\) が正方行列のとき(本問の(1)がそうである)、まずその行列式を計算するのだ!
そして、行列式の値が \(\ne 0\) ならば、\(f_A\) は『全単射』確定である。
なぜなら、\(|A| \ne 0\) ならば、\(A^{-1}\) が存在するからである。
すると、\(A\boldsymbol{x}=A\boldsymbol{y}\) ならば、左から \(A^{-1}\) かけて \(\boldsymbol{x}=\boldsymbol{y}\) がでて、\(f_A\) は単射であることが出るし、任意の \(\boldsymbol{b} \in \mathbb{R^{3}}\) に対して、\(\boldsymbol{x}=A^{-1}\boldsymbol{b} \in \mathbb{R^{3}}\) をとれば、\(f_A(\boldsymbol{x})=\boldsymbol{b}\) となって、\(f_A\) は全射であることが出る。
行列 \(A\) が正方行列で \(|A|=0\) のとき、または \(A\) が正方行列でないとき
そして、正方行列 \(A\) の行列式の値が \(0\)、 または、そもそも行列 \(A\) が正方行列でないときは \(rankA\) を求めるのだ。
ここで、次の最重要公式の出番となるのだ!
次元公式:『 \(dim(Kerf_A)+dim(Imf_A)=(定義域の次元)\) 』
次の公式は、線形代数学においてとても重要なものである。証明はとりあえず置いといて、その意味と使い方をまずマスターしよう!
$$dim(Kerf_A)+dim(Imf_A)=(定義域の次元) \cdots (\star)$$
ここで、公式の右辺について、\(A\) が正方行列のときは、定義域の次元は行列の列数(または行数)に等しい(本問の場合は3)。また、\(A\) が正方行列でないときは、定義域の次元は行列の列数に等しくなることに注意だ。
たとえば、(2)の行列 \(A\) は \(3 \times 4\) 行列なので、\(f_A : \mathbb{R^{4}} \longrightarrow \mathbb{R^{3}}\) となって、定義域の次元は列数の4に等しくなる。
公式 \((\star)\) をマスターすると、\(f_A\) を完璧に分析できるようになるのだ。
念のため、公式 \((\star)\) についてもう少しくわしく説明しておこう。
以下の説明は一般の、\(f_A : \mathbb{R^{n}} \longrightarrow \mathbb{R^{m}}\) に対してのものである。(\(A\) は \(m \times n\) 行列)
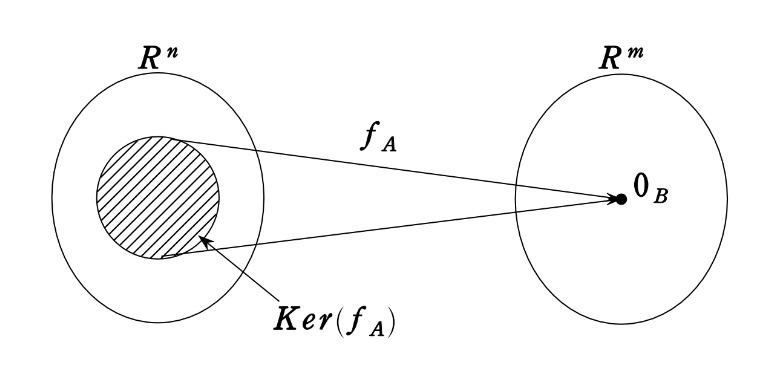
まず、左辺の \(Kerf_A\) について、これは 『\(f_A\) の核』と呼び、その定義は、$$Kerf_A=\{\boldsymbol{x} \in \mathbb{R^{n}}| f_A(\boldsymbol{x})=\boldsymbol{0}\}$$である。つまり、\(\mathbb{R^{m}}\) の零元 \(0\) に飛ぶような \(\mathbb{R^{n}}\) の元全体である。(カッコを用いて、\(Ker(f_A)\) と書いてもよい。)
\(Kerf_A\) は、\(\mathbb{R^{n}}\) の部分空間となることが簡単に示される。
(\(\boldsymbol{x}、\boldsymbol{y} \in Kerf_A \Longrightarrow \boldsymbol{x}+\boldsymbol{y} \in Kerf_A \)であることと、
\(\alpha \in \mathbb{R}\ (or\ \mathbb{C}) 、\boldsymbol{x} \in Kerf_A \Longrightarrow \alpha\boldsymbol{x} \in Kerf_A\) であることをチェックする!)
よって、\(Kerf_A\) の次元が考えられ、その次元を \(dim(Kerf_A)\) と表しているのだ。
(\(dim\) は次元の英単語:\(dimension\) から来てるぞ。)

次に、左辺の \(Imf_A\) について、これは 『\(f_A\) の像』と呼び、その定義は、$$Imf_A=\{f_A(\boldsymbol{x}) \in \mathbb{R^{m}}| \boldsymbol{x} \in \mathbb{R^{n}}\}$$である。つまり、定義域である \(\mathbb{R^{n}}\) の元全体の行く先である。
\(Imf_A\) は、\(\mathbb{R^{m}}\) の部分空間となることが簡単に示される。
(\(\boldsymbol{x}、\boldsymbol{y} \in Imf_A \Longrightarrow \boldsymbol{x}+\boldsymbol{y} \in Imf_A \)であることと、
\(\alpha \in \mathbb{R}\ (or\ \mathbb{C}) 、\boldsymbol{x} \in Kerf_A \Longrightarrow \alpha\boldsymbol{x} \in Imf_A\) であることをチェックする!)
よって、\(Imf_A\) の次元が考えられ、その次元を \(dim(Imf_A)\) と表しているのだ。
つまり、公式 \((\star)\) が主張していることは、『\(Kerf_A\) の次元と \(Imf_A\) の次元の和は、定義域の次元に等しい』ということなのだ。
これで公式の意味は分かっただろう。次にこの公式の使い方について説明しよう。
次元公式の使い方
さて、我々は \(|A|=0\) のとき、あるいは行列 \(A\) が正方行列ではない場合を考えているのであった。
この場合、\(A\) のランクを求めることはすでに言った通りである。例えば、\(rankA=\ell (\ell は自然数)\) だった場合を考えてみよう。
\(rankA\) について次の事実がある。
『ランクというのは、1次独立である列ベクトル(あるいは行ベクトル)の最大個数である。』
この事実から得られることは、$$rankA=dim(Imf_A)$$である。つまり、\(A\) のランクを求めることは、\(dim(Imf_A)\) を求めることになるということだ!
(少々理論的なことは端折ってしまったが、しっかりやろうとするとだいぶ本筋からそれてしまう恐れがあるので、ここではまず、問題の解き方に焦点を当てたいと思う。)
さて、\(rankA=\ell\) が分かったら、公式 \((\star)\) により、\(dim(Imf_A)=\ell\) を代入して、$$dim(Kerf_A)+\ell=n$$$$dim(Kerf_A)=n-\ell$$となって、\(dim(Kerf_A)\) も求められるのだ。
要するに言いたかったことは、『公式 \((\star)\) を使うことによって、\(rankA\) さえ求めれば、\(f_A\) の全貌を教えてくれる』ということだ。
前置きが長くなったが、これから、問題の解答に入りたいと思う。
問題の解答
(1) \(A=\begin{pmatrix}1&0&-1\\1&1&0\\-1&1&-1\end{pmatrix}\) は正方行列なので、まず、\(A\) の行列式を求める。
\(|A|=-1-1-(1+0)=-3 (\ne 0)\)より、はい、\(f_A\) は全単射確定である。
このように行列 \(A\) が正方行列の場合、まずその行列式を計算するのが一番早いことが多い。
\(|A|=0\) となる場合も1問やりたいところだが、実質的には次の (2) の解答と同じなのでそちらを参照してほしい。
(2) \(A=\begin{pmatrix}-3&3&2&4\\1&-1&0&-2\\0&1&1&1\end{pmatrix}\) は正方行列ではないので、まず \(A\) のランクを求める。
\begin{matrix}-3&3&2&4\\1&-1&0&-2\\0&1&1&1\end{matrix}
第2行に3を掛けて第1行に加えて、
\begin{matrix}0&0&2&-2\\1&-1&0&-2\\0&1&1&1\end{matrix}
第1行に \(\frac{1}{2}\) を掛け、第2行に第3行を加えて、
\begin{matrix}0&0&1&-1\\1&0&1&-1\\0&1&1&1\end{matrix}
第1行を第3行に移動して、
\begin{matrix}1&0&1&-1\\0&1&1&1\\0&0&1&-1\end{matrix}
第1行から第3行を引き、第2行から第3行を引いて、
\begin{matrix}1&0&0&0\\0&1&0&2\\0&0&1&-1\end{matrix}
したがって、\(rankA=3\) である。
公式より、$$dim(Kerf_A)+dim(Imf_A)=4 (←Aの列数)$$ここで、\(dim(Imf_A)=rankA=3\) を代入して、$$dim(Kerf_A)+3=4$$$$dim(Kerf_A)=4-3=1$$
したがって、\(f_A\) は単射ではない。(\(f_A\) は線形写像なので、\(f_A\) が単射であることと、\(Kerf_A=\{\boldsymbol{0}\}\) であることは同値であった。よって、『\(f_Aが単射 \Longleftrightarrow dim(Kerf_A)=0 \)』がいえるのだ。
一方で、\(dim(Imf_A)=rankA=3\) は値域の次元 \(dim(\mathbb{R^{3}})=3\) に等しいので、
\(f_A\) は全射となる \(\cdots (答)\)。
これで問題の解答は終わった。いかがだっただろうか? 実際に問題を解くうえで必要となるのは、\(A\) のランクの値と、次元公式の知識だけである。
最初に、『解き方が決まっている』と言った意味が、今は分かるのではないだろうか?
ちなみに、上の(2)において、もしも \(rankA=2\) だった場合はどうなるのか考えてほしい。
次元公式より、\(dim(Kerf_A)+2=4\) より、\(dim(Kerf_A)=2\) となる。したがって、\(f_A\) は単射ではないし、\(dim(Imf_A)=rankA=2<3 (=dim(\mathbb{R^{3}}))\) であるから、\(f_A\) は全射でもない、ということになる。このような単射でも全射でもない写像も多く存在することも知っておいて損はないだろう。
行列によって定まる線形写像 \(f_A\) について、行列 \(A\) が正方行列のときは、とりあえず \(|A|\) を計算し、\(|A|=0\) または行列 \(A\) が正方行列でないときは、\(rankA\) を計算し、次元公式:\(dim(Kerf_A)+dim(Imf_A)=(定義域の次元)\) を利用する。
問題.18 解答
問題.17の(2)行列は、$$A=\begin{pmatrix}-3&3&2&4\\1&-1&0&-2\\0&1&1&1\end{pmatrix}$$で、正方行列ではないからそのランクを求めたのであった。ここまでは同じである。その結果は、
\begin{matrix}1&0&0&0\\0&1&0&2\\0&0&1&-1\end{matrix}となって、\(rankA=3\) となった。この \(A\) を簡約化した行列を \(\tilde{A}\) と書こう。
つまり、\(\tilde{A}=\begin{pmatrix}1&0&0&0\\0&1&0&2\\0&0&1&-1\end{pmatrix}\) だ。さて、核の基底の求め方だが、この行列 \(\tilde{A}\) を用いるのだ。
核の定義は、\(Kerf_A=\{\boldsymbol{x} \in \mathbb{R^{4} | f_A(\boldsymbol{x})=\boldsymbol{0}}\}\) であった。よって、\(A\boldsymbol{x}=\boldsymbol{0}\)を満たす \(\boldsymbol{x}\) を求めることにになるわけだが、実は、$$A\boldsymbol{x}=\boldsymbol{0} \Longleftrightarrow \tilde{A}\boldsymbol{x}=\boldsymbol{0} \cdots (\star)$$がいえるのである。
このことを理解するには、連立方程式を解くときに行う加減法を思い出して欲しい。加減法というのは、ある式にある数を掛けて別の式に足す、ということを何回か実行しても解は変化しないのであった。
行列の基本変形というのはこの加減法と同じことをしているに過ぎないので、\((\star)\) は成り立つのである。
さて、\(\tilde{A}\boldsymbol{x}=\boldsymbol{0}\) は、
\(\begin{pmatrix}1&0&0&0\\0&1&0&2\\0&0&1&-1\end{pmatrix}\boldsymbol{x}=\boldsymbol{0} \Longleftrightarrow \begin{cases}x=0\\y+2w=0\\z-w=0 \end{cases}\)
(ただし、\(\boldsymbol{x}=^{t}\!\!(x , y , z , w)\) と置いた。)と書けるので、
これより、\(x=0\)、\(w=t (t \in \mathbb{R}\ (or\ \mathbb{C}))\) とすると、\(y=-2t\)、
よって、$$\boldsymbol{x}=\left(\begin{array}{c}x\\y\\z\\w\end{array}\right)=t\left(\begin{array}{c}0\\-2\\1\\1\end{array}\right) (t \in \mathbb{R}\ (or\ \mathbb{C}))$$となって、無限個の解をもつことが分かったのだ。すなわち、求める『核に基底』は、$$\boldsymbol{x}=\left(\begin{array}{c}0\\-2\\1\\1\end{array}\right) \cdots (答) $$となる。次元というのは基底の個数でもあるのでこの結果は、問題.17で求めた次元が1であることにも合致している。
次に、\(f_A\) の『像の基底』を求める。問題.17により、\(f_A\) は全射であることが分かった。
よって、とにかく \(f_A\) の像 \(f_A(\mathbb{R^{4}})\) は、 \(\mathbb{R^{3}}\) に一致することがいえる。
さて、\(f_A\) の像の定義は、\(Imf_A=\{A\boldsymbol{
x} \in \mathbb{R^{3}} | \boldsymbol{x} \in \mathbb{R^{4}}\}\) であった。ここで、\(A\boldsymbol{x}\) について、行列 \(A\) を列ベクトルを用いて表すと、\(A=(\boldsymbol{a_1} \boldsymbol{a_2} \boldsymbol{a_3} \boldsymbol{a_4})\) となるから、$$(\boldsymbol{a_1} \boldsymbol{a_2} \boldsymbol{a_3} \boldsymbol{a_4})\boldsymbol{x}=(\boldsymbol{a_1} \boldsymbol{a_2} \boldsymbol{a_3} \boldsymbol{a_4})\left(\begin{array}{c}x\\y\\z\\w\end{array}\right)$$$$=\boldsymbol{a_1}x+\boldsymbol{a_2}y+\boldsymbol{a_3}z+\boldsymbol{a_4}w$$と書ける。
これら \(\boldsymbol{a_1}、\boldsymbol{a_2}、\boldsymbol{a_3}、\boldsymbol{a_4}\) のうち、1次独立である列ベクトルを求めるのが目標だ。その1次独立である列ベクトルの個数が『像の次元』となるのだ。
ここでまた、行列 \(A\) の簡約化 \(\tilde{A}\) の出番である。
\(\tilde{A}=\begin{pmatrix}1&0&0&0\\0&1&0&2\\0&0&1&-1\end{pmatrix}\)であった。
行列 \(\tilde{A}\) を列ベクトルを用いて表したものを、\(A=(\tilde{\boldsymbol{a_1}} \tilde{\boldsymbol{a_2}} \tilde{\boldsymbol{a_3}} \tilde{\boldsymbol{a_4}})\) としよう。
そうすると、すぐに $$\tilde{\boldsymbol{a_4}}=2\tilde{\boldsymbol{a_2}}-\tilde{\boldsymbol{a_3}}$$と表せることに気づくだろう。
つまり、\(\tilde{\boldsymbol{a_1}}、\tilde{\boldsymbol{a_2}}、\tilde{\boldsymbol{a_3}}、\tilde{\boldsymbol{a_4}}\) のうち、1次独立であるのは、\(\tilde{\boldsymbol{a_1}}、\tilde{\boldsymbol{a_2}}、\tilde{\boldsymbol{a_3}}\) だということだ。
ここで、核の基底を求めるときに紹介した$$A\boldsymbol{x}=\boldsymbol{0} \Longleftrightarrow \tilde{A}\boldsymbol{x}=\boldsymbol{0} \cdots (\star)$$を思い出してほしい。この \((\star)\) を書き換えると、$$\boldsymbol{a_1}x+\boldsymbol{a_2}y+\boldsymbol{a_3}z+\boldsymbol{a_4}w=\boldsymbol{0} \Longleftrightarrow \tilde{\boldsymbol{a_1}}x+\tilde{\boldsymbol{a_2}}y+\tilde{\boldsymbol{a_3}}z+\tilde{\boldsymbol{a_4}}w=\boldsymbol{0}$$となるだろう。
これから何が言えるのかというと、『\(\tilde{\boldsymbol{a_1}}、\tilde{\boldsymbol{a_2}}、\tilde{\boldsymbol{a_3}}、\tilde{\boldsymbol{a_4}}\) のうち、1次独立であるのは、\(\tilde{\boldsymbol{a_1}}、\tilde{\boldsymbol{a_2}}、\tilde{\boldsymbol{a_3}}\) である』ということと、『\({\boldsymbol{a_1}}、{\boldsymbol{a_2}}、{\boldsymbol{a_3}}、{\boldsymbol{a_4}}\) のうち、1次独立であるのは、\({\boldsymbol{a_1}}、{\boldsymbol{a_2}}、{\boldsymbol{a_3}}\) である』ことは同値であるということだ。
したがって、\(\tilde{\boldsymbol{a_4}}=2\tilde{\boldsymbol{a_2}}-\tilde{\boldsymbol{a_3}}\) と表されるということは、\(\boldsymbol{a_4}=2\boldsymbol{a_2}-\boldsymbol{a_3}\) と表されることになるのだ!
今、\(\tilde{\boldsymbol{a_1}}、\tilde{\boldsymbol{a_2}}、\tilde{\boldsymbol{a_3}}\) が1次独立であったとしよう。このとき我々の目標は、\(\boldsymbol{a_1}、\boldsymbol{a_2}、\boldsymbol{a_3}\)が1次独立であることを示すことである。つまり、$$x_1\boldsymbol{a_1}+x_2\boldsymbol{a_2}+x_3\boldsymbol{a_3}=\boldsymbol{0} \Longrightarrow x_1=x_2=x_3=0$$を示すことである。
$$x_1\boldsymbol{a_1}+x_2\boldsymbol{a_2}+x_3\boldsymbol{a_3}=\boldsymbol{0}$$ と仮定する。これは、$$x_1\boldsymbol{a_1}+x_2\boldsymbol{a_2}+x_3\boldsymbol{a_3}+0\cdot \boldsymbol{a_4}$$$$\Longleftrightarrow (\boldsymbol{a_1} \boldsymbol{a_2} \boldsymbol{a_3} \boldsymbol{a_4})\left(\begin{array}{c}x_1\\x_2\\x_3\\0\end{array}\right)=\boldsymbol{0}$$$$\Longleftrightarrow A\left(\begin{array}{c}x_1\\x_2\\x_3\\0\end{array}\right)=\boldsymbol{0}$$と書ける。
$$A\boldsymbol{x}=\boldsymbol{0} \Longleftrightarrow \tilde{A}\boldsymbol{x}=\boldsymbol{0} \cdots (\star)$$によって、これは、$$\Longleftrightarrow \tilde{A}\left(\begin{array}{c}x_1\\x_2\\x_3\\0\end{array}\right)=\boldsymbol{0}$$と同値である。
これを変形すると、$$x_1\tilde{\boldsymbol{a_1}}+x_2\tilde{\boldsymbol{a_2}}+x_3\tilde{\boldsymbol{a_3}}=\boldsymbol{0}$$となって、仮定により \(\tilde{\boldsymbol{a_1}}、\tilde{\boldsymbol{a_2}}、\tilde{\boldsymbol{a_3}}\) は1次独立であるから、
\(x_1=x_2=x_3=0\) を得る。ゆえに、\(\boldsymbol{a_1}、\boldsymbol{a_2}、\boldsymbol{a_3}\) は1次独立である。\(q.e.d.\)
実際に、\(\boldsymbol{a_4}=\left(\begin{array}{c}4\\-2\\1\end{array}\right)=2\left(\begin{array}{c}3\\-1\\1\end{array}\right)-\left(\begin{array}{c}2\\0\\1\end{array}\right)=2\boldsymbol{a_2}-\boldsymbol{a_3}\) となって確かに成り立つ。
したがって、求める『像の基底』は、$$\{\boldsymbol{a_1}、\boldsymbol{a_2}、\boldsymbol{a_3}\}$$すなわち、
$$\left\{\begin{pmatrix}-3\\1\\0 \end{pmatrix}、\begin{pmatrix}3\\-1\\1 \end{pmatrix}、\begin{pmatrix}2\\0\\1 \end{pmatrix} \right\} \cdots (答)$$となる。(この結果は、問題.17でもとめた像の次元が3であることに合致する。)
ようするに、『像の次元』を求めるには \(A\) を簡約化し、どの列ベクトルが他のベクトルを用いて表されるかを見つければよいのだ。
行列によって定まる線形写像 \(f_A\) について、行列 \(A\) が正方行列でないときは、\(A\) を簡約化した行列 \(\tilde{A}\) を求める。
そして、\(Kerf_A\) の基底を求めるときは、\(\tilde{A}\boldsymbol{x}=\boldsymbol{}0\) を解き、
\(Imf_A\) の基底を求めるときは、\(\tilde{A}\)の列ベクトルの中で1次独立なものを見つける。



コメント