第4回 解答
問題.10 解答
$$\boldsymbol{a}=\left( \begin{array}{c}1\\3\\2 \end{array} \right)、\boldsymbol{b}=\left( \begin{array}{c}2\\-2\\1 \end{array} \right)$$の外積を計算する際、公式を頑張って暗記してもよいが、私は次のようにやっているぞ。その名も『たすき掛けアタック』だ!
まず、与えられた列ベクトルを右下図のように左右に並べるが、第一成分だけ余分に一番下に付け足しておくのだ!なぜこんなことするのかって?それは、そうするとうまくいくからだ!
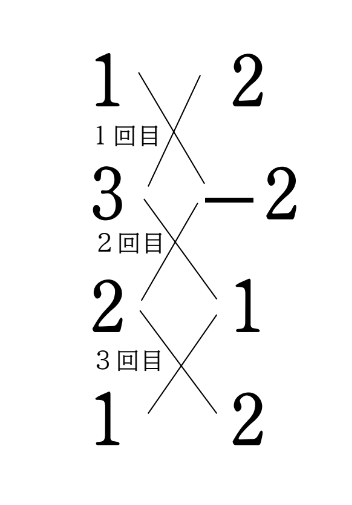
並べたら上から順にたすき掛けを3回していき、外積の成分を求めていくのだ。※外積は、\(\boldsymbol{a}、\boldsymbol{b}\) と同じくベクトルとなるぞ。
ここで、一つだけ注意すべきは、1回目の×印によるたすき掛けの結果が第3成分となり、2回目の×印によるたすき掛けの結果が第1成分となり、3回目の×印によるたすき掛けの結果が第2成分となるということだ。
つまり、たすき掛けの結果は上から順にいえば、第3成分、第1成分、第2成分ということになる。
ちょっとややこしいが、外積は『3成分,1成分,2成分』の順だということを口ずさんで覚えてほしい。
解答は、次のようになる。$$\big(3\cdot1-(-2)\cdot2 , 2\cdot2-1\cdot1 , 1\cdot(-2)-2\cdot3\big)=(7 , 3 , -8)$$
さて、外積の計算自体はこのように簡単にできる。大切なのは外積の意味なのだ。
とりあえず、今求めた外積と与えられた二つのベクトルの内積をそれぞれ計算してみてほしい。どうなるだろうか?
$$(\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{a}=^{t}\!(7 , 3 , -8)\cdot ^{t}\!(1 , 3 , 2)=7+9-16=0$$
$$(\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{b}=^{t}\!(7 , 3 , -8)\cdot ^{t}\!(2 , -2 , 1)=14-6-8=0$$
気づいただろうか?内積が0ということは、二つのベクトルは直交しているということである。つまり、\(\boldsymbol{a}\) と \(\boldsymbol{b}\) の外積は、\(\boldsymbol{a}\) と \(\boldsymbol{b}\) に直交するということだ!
この状況を図示すると下図のようになる。
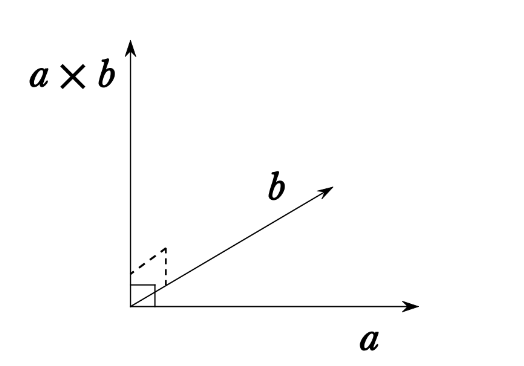
このことは、とても大事なことなので忘れずにいてほしい。
\(\boldsymbol{a}\) と \(\boldsymbol{b}\) の外積:\(\boldsymbol{a}\times\boldsymbol{b}\) は、\(\boldsymbol{a}\) と \(\boldsymbol{b}\) に直交する
問題.11 解答
まず、\(\boldsymbol{a}=(1 , 3 , 2)\) 、 \(\boldsymbol{b}=(2 , -2 , 1)\)、\(\boldsymbol{c}=(-2 , 1 , 1)\) とおくと、\(\boldsymbol{a}\) と \(\boldsymbol{b}\) は前問の \(\boldsymbol{a}\) と \(\boldsymbol{b}\) であることに注意する。
問題の解答の前に、外積に関する重要公式を二つ紹介したい。外積についてはこの二つだけ知っておけば十分だ。下の公式において、\(\boldsymbol{a}=(a_1 , a_2 , a_3)、\boldsymbol{b}=(b_1 , b_2 , b_3)、\boldsymbol{c}=(c_1 , c_2 , c_3)\) とおいた。
$$ |\boldsymbol{a}\times\boldsymbol{b}|=|\boldsymbol{a}||\boldsymbol{b}|sin\theta (\theta は \boldsymbol{a} と \boldsymbol{b} のなす角で、0 \le \theta \le \pi)\cdots(\star1) $$
$$ (\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c}=\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix} \cdots (\star2)$$
いずれの公式も目新しいだろう?
公式 \((\star1)\) の例えば、\(|\boldsymbol{a}|\) は、ベクトルの大きさ(つまり長さ)を表していて、数に使う絶対値記号とは意味が違うことに注意してほしい。また、\((\star2)\) の \(『\cdot』\) 記号は内積を表すぞ。
証明は、\((\star1)\) については、定義に従ってゴリゴリやればできるし、\((\star2)\) については、前回の行列式の解説パートで紹介した余因子展開を使えばできる。ただ、少し長めの証明となっていて、問題の本筋からそれてしまう恐れがあるので、下のアコーディオンボックスにまとめておいた。証明を見るかどうかはお任せしよう。
※証明は一行一行覚えようとするのではなく(そんなことをしてもすぐに忘れてしまうのがオチ)、大体の流れをつかむ程度で十分だ。ああ、こういうことをやって証明しているのか、というくらいがちょうど良い。
定義通りにゴリゴリ計算していくぞ。
まず、前問で紹介した『たすき掛けアタック』を使って、\(\boldsymbol{a}\) と \(\boldsymbol{b}\) の外積の大きさの2乗を計算すると、
$$|\boldsymbol{a}\times\boldsymbol{b}|^{2}=(a_2b_3-b_2a_3)^{2}+(a_3b_1-b_3a_1)^{2}+(a_1b_2-b_1a_2)^{2}$$となるだろう。右辺を展開すると、
\((a_2^{2}b_3^{2}-2a_2a_3b_2b_3+b_2^{2}a_3^{2})\)
\(+(a_3^{2}b_1^{2}-2a_1a_3b_1b_3+b_3^{2}a_1^{2})\)
\(+(a_1^{2}b_2^{2}-2a_1a_2b_1b_2+b_1^{2}a_2^{2})\)
となる。
次に、\(a_2^{2}b_2^{2}、a_3^{2}b_3^{2}、a_3^{2}b_3^{2}\) を足して引いてすると、
\(a_2^{2}(b_1^{2}+b_2^{2}+b_3^{2})-a_2^{2}b_2^{2}-2a_2a_3b_2b_3\)
+\(a_3^{2}(b_1^{2}+b_2^{2}+b_3^{2})-a_3^{2}b_3^{2}-2a_1a_3b_1b_3\)
+\(a_1^{2}(b_1^{2}+b_2^{2}+b_3^{2})-a_1^{2}b_1^{2}-2a_1a_2b_1b_2\)
\(=(a_1^{2}+a_2^{2}+a_3^{2})(b_1^{2}+b_2^{2}+b_3^{2})-(a_1b_1+a_2b_2+a_3b_3)^{2}\cdots①\)
となるだろう。\(a_1b_1+a_2b_2+a_3b_3\) が、\(\boldsymbol{a}\) と \(\boldsymbol{b}\) の内積を表していることに注意すると、定義より、
\(a_1b_1+a_2b_2+a_3b_3=|\boldsymbol{a}||\boldsymbol{b}|cos\theta\) と書ける。
よって、\(①=|\boldsymbol{a}|^{2}|\boldsymbol{b}|^{2}-(|\boldsymbol{a}||\boldsymbol{b}|cos\theta)^{2}=|\boldsymbol{a}|^{2}|\boldsymbol{b}|^{2}(1-cos^{2}\theta)=|\boldsymbol{a}|^{2}|\boldsymbol{b}|^{2}sin^{2}\theta\)
両辺の2乗を取って、\((\star1)\) を得る。
\((\star2)\)について:
こちらの証明は、前回の解説で紹介した『余因子展開』を使うぞ。
\( (\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c}=\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix} \) において、右辺の行列式を第3列に関して展開すると、
右辺にぴったり一致するぞ!実際に第3列に関して展開してみると、
$$\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}=c_1\begin{vmatrix}a_2&b_2\\a_3&b_3\end{vmatrix}-c_2\begin{vmatrix}a_1&b_1\\a_3&b_3\end{vmatrix}+c_2\begin{vmatrix}a_1&b_1\\a_2&b_2\end{vmatrix}$$$$=c_1(a_2b_3-b_2a_3)-c_2(a_1b_3-b_1a_3)+c_3(a_1b_2-b_1a_2)=(\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c}$$となって \((\star2)\) を得る。
これで証明が完了だ。少し長くて大変だったが、大体の流れさえつかめれば全然OKだ。
これで、 \((\star1)\)と\((\star1)\)が示された。もう一度書くと、$$ |\boldsymbol{a}\times\boldsymbol{b}|=|\boldsymbol{a}||\boldsymbol{b}|sin\theta (\theta は \boldsymbol{a} と \boldsymbol{b} のなす角で、0 \le \theta \le \pi)\cdots(\star1) $$
$$ (\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c}=\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix} \cdots (\star2)$$
さて、準備が整ったので問題の解答に入ろう。
まず、平行六面体の体積はもちろん、『底面積×高さ』で求められる。
先に『底面積』について見ていこう。\( |\boldsymbol{a}\times\boldsymbol{b}|=|\boldsymbol{a}||\boldsymbol{b}|sin\theta (0 \le \theta \le \pi) \cdots (\star1) \) をもう一度見てほしい。何か気づかないだろうか?
そう!右辺の \( |\boldsymbol{a}||\boldsymbol{b}|sin\theta\) は \(\boldsymbol{a}\) と\(\boldsymbol{b}\) で張られる平行四辺形の面積を表しているではないか!
つまり、\(\boldsymbol{a}\) と \(\boldsymbol{b}\) の外積の大きさは、\(\boldsymbol{a}\) と \(\boldsymbol{b}\) で張られる平行四辺形の面積に等しいのである。これが、\((\star1)\) の真の意味である。そして、その外積は前問で \(\boldsymbol{a}\times\boldsymbol{b}=^{t}\!(7 , 3 , -8) \) と求めていた。したがって、その大きさは、$$|^{t}\!(7 , 3 , -8)|=\sqrt{7^{2}+3^{2}+(-8)^{2}}=\sqrt{122}$$これが、\(\boldsymbol{a}=(1 , 3 , 2)\) と \(\boldsymbol{b}=(2 , -2 , 1)\) で張られる平行四辺形の面積となる。
残るは、『高さ』についてである。前問より、\(\boldsymbol{a}\times\boldsymbol{b}\) は、\(\boldsymbol{a}\) と \(\boldsymbol{b}\) に垂直であった。
よって、平行六面体の高さは、\(\boldsymbol{a}\times\boldsymbol{b}\) と、\(\boldsymbol{c}\) のなす角を \(\theta\) とおくとき、\(|\boldsymbol{c}||cos\theta|\) で与えられるだろう。 下図参照。
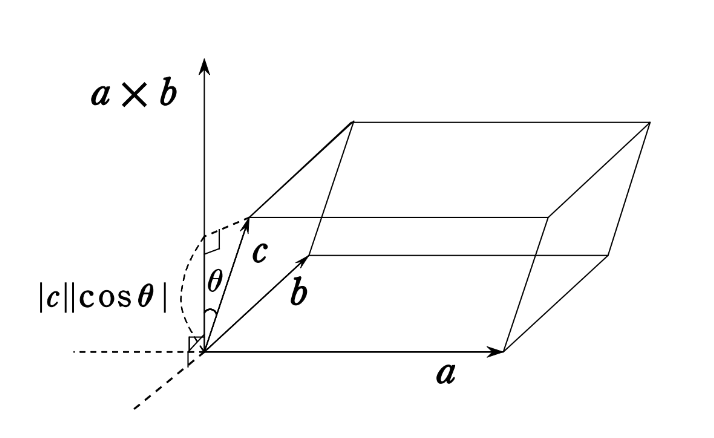
したがって、平行六面体の体積は、とりあえず、$$(底面積)\times(高さ)=|\boldsymbol{a}\times\boldsymbol{b}|\times |\boldsymbol{c}||cos\theta| ( \theta は \boldsymbol{a} \times \boldsymbol{b} と、\boldsymbol{c} のなす角)$$で与えられることになるだろう。
ここで、上で示した$$(\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c}=\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix} \cdots (\star2)$$をもう一度見てほしい。
何か気づかないだろうか?
そう! 左辺は内積の定義から、$$(\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c}=|\boldsymbol{a}\times\boldsymbol{b}|\times |\boldsymbol{c}|cos\theta$$と書けるので、この絶対値を取れば、$$|\boldsymbol{a}\times\boldsymbol{b}|\times |\boldsymbol{c}||cos\theta|$$となって、\(\boldsymbol{a}\) と \(\boldsymbol{b}\) と \(\boldsymbol{c}\) で張られる平行六面体の体積を表すではないか!
これが右辺に等しいということは、すなわち、平行六面体の体積は、\(\boldsymbol{a}\) と \(\boldsymbol{b}\) と \(\boldsymbol{c}\) を列に持つ3×3行列の、行列式の絶対値に等しい、ということだ。
したがって、問題の答えは、$$\left|det\begin{pmatrix}1&2&-2\\3&-2&1\\2&1&1\end{pmatrix}\right|= |-2+4-6-(8+1+6)|=|-4-15|=19$$となる。
どうだっただろうか? 色々ややこしかったと思うが言いたかったことは、3次元空間において平行四辺形の面積と平行六面体の面積は、それぞれ『外積の大きさ』と、『行列式の絶対値』に対応しているということだ。
以上のことをまとめると、次のようになる。
3次元空間において、
・\(\boldsymbol{a}\) と \(\boldsymbol{b}\) 張られる平行四辺形の面積は、\(|\boldsymbol{a}\times\boldsymbol{b}|\)で与えられ、
・\(\boldsymbol{a}\) と \(\boldsymbol{b}\) と \(\boldsymbol{c}\) で張られる平行六面体の体積は、\(\left|det\begin{pmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{pmatrix}\right|\)で与えられる。
※最初から上の証明まで含めた理論的な内容をすべて理解する必要な全くない。今は、上記の二つだけ押さえておいて、問題を解くことを楽しんでほしい。(上記二つの知識だけで、今回のタイプの問題は解けるのである)
理論的な内容は気なったときにちょっと振り返ってみて、「ああ、こんなことしてたな、すごいなぁ」くらいに味わってもらえればいいのである。あまり理論的な内容を根詰めてやると、数学は辛いものになってしまい全く長続きしない。ただ、理論的な内容を全く無視するわけにもいかない。大事なのは適度に『味わう』という精神なのである。そうすれば段々と慣れてきて、『味わい方』が深くなってくるだろう。ぜひ、長く続けられるような精神を培ってほしい。
問題.12 解答
今回の最後を飾る問題は、行列式に関する証明問題だ。行列式の性質と、余因子展開を組み合わせてスマートに証明できるぞ。
(証明)
与式の左辺の行列式を第1行に関して展開すると、$$ax+by+cz+d=0 (a , b , c , d \in \mathbb{R})\cdots①$$と書ける。
①は空間における平面を表している。ここで、行列式の性質(二つの行が等しければ行列式の値は0)より、元の行列式に \((x , y , z)=(x_0 , y_0 , z_0)、(x_1 , y_1 , z_1)、(x_2 , y_2 , z_2)\) を代入すると、それぞれすべて0になるので、①も然りとなる。
すなわち、①は \(P_0、P_1、P_2\) を通る平面となる。 \(q.e.d\)
上の証明において、①が平面であることを言うには厳密には、\((a , b , c)\ne(0 , 0 , 0)\) であることを言わなければならないが、これは仮定の3点、 \(P_0(x_0 , y_0 , z_0)、P_1(x_1 , y_1 , z_1)、P_2(x_2 , y_2 , z_2)\) が同一直線上にないことからいえるのである。



コメント