このページでは、簡単そうに見えて実は非常に骨のある『角度を求める問題』を集めました。
普通の問題ではもはや刺激を感じられなくなってしまった猛者のみなさん、
ぜひ挑戦してみてください!
第一問
下の図において、AC=BD、∠ACB=20°、∠ADB=40°のとき∠\(x\)を求めよ。
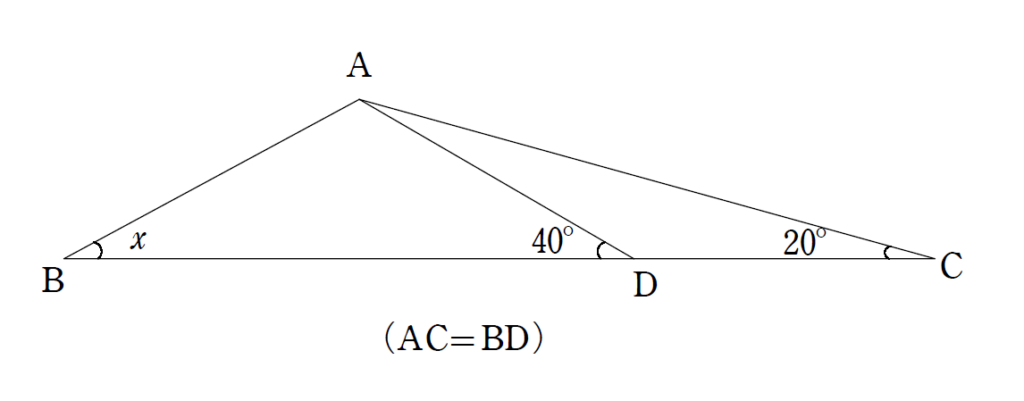
辺ACを一辺とする正三角形を描く。
または、辺CDを一辺とする正三角形を描く。
または、辺CDを一辺とする正三角形を描く。
\(x=30°\)
解説は後々動画をアップしたいと思うのでしばしお待ちください!
第二問
下の図において、AB=AC=CD , ∠BAC=100° , ∠ACD=20°のとき∠\(x\)を求めよ。
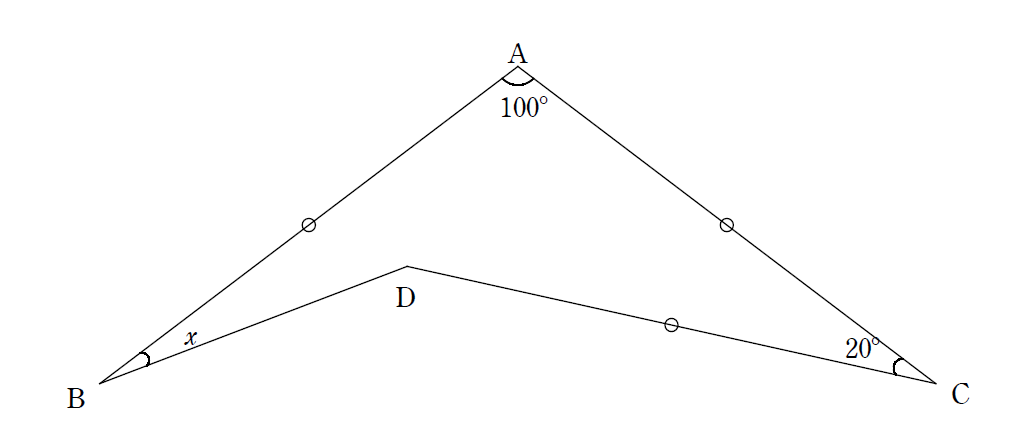
辺ACを一辺とする正三角形を描く。
\(x=10°\)
解説は後々動画をアップしたいと思うのでしばしお待ちください!
第三問
下の図において、辺BCの中点をD , ∠CAD=15° , ∠ADB=45°のとき、∠\(x\)を求めよ。
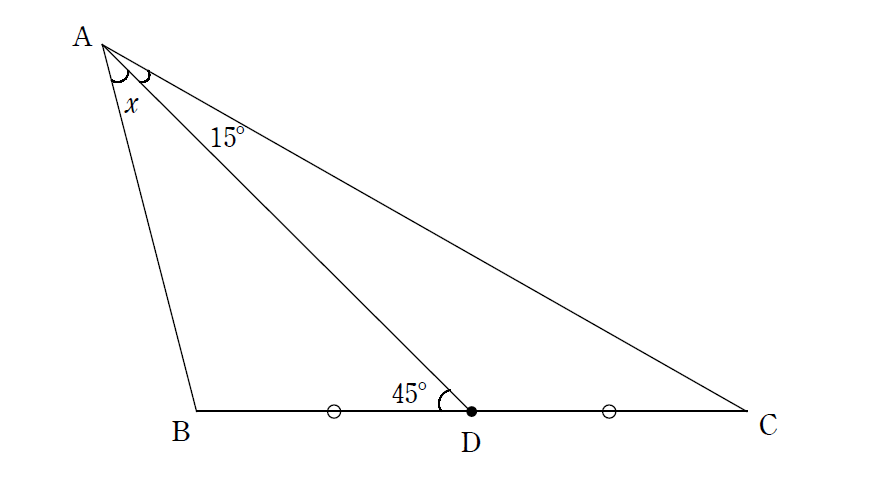
辺BDを一辺とする正三角形を描く。
\(x=30°\)
解説は後々動画をアップしたいと思うのでしばしお待ちください!
第四問
下の図において、AB=CD , ∠ABC=40° , ∠ACB=20°のとき、∠\(x\)を求めよ。
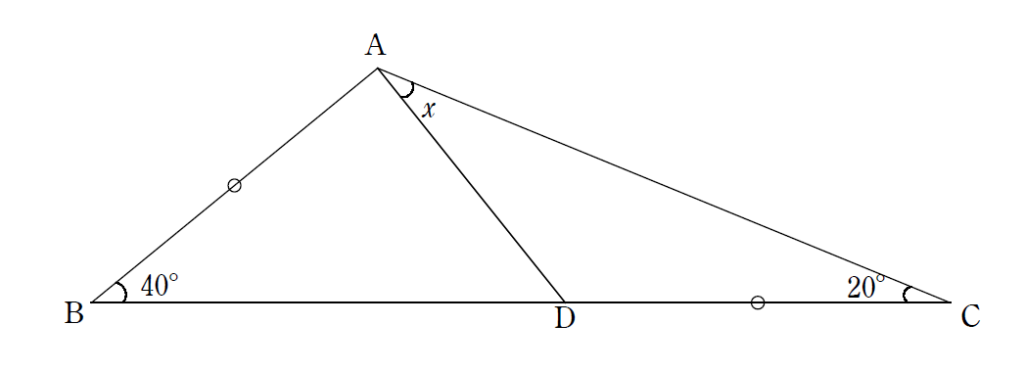
∠ABCの二等分線を引く。
\(x=20°\)
解説は後々動画をアップしたいと思うのでしばしお待ちください!
第五問
下の図の平行四辺形ABCDにおいて、∠ACB=30° , ∠DBC=15°
のとき∠\(x\)を求めよ。
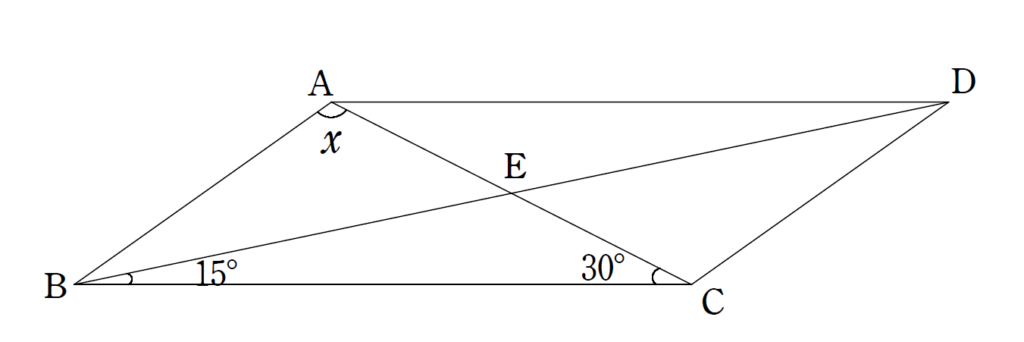
Aから辺BCの降ろした垂線の足をHとする。
そして、三角形AHEを考える。
そして、三角形AHEを考える。
\(x=105°\)
解説は後々動画をアップしたいと思うのでしばしお待ちください!
まとめ
いかがだったでしょうか?なかなか苦戦を強いられたことと想像します。(自分がそうでした)
さて、上記問題を解いていて何か気づいたことはありますか?
それは、問題を解く上でのカギとなる考えです。これを意識してるかしてないかによって、全く変わってきます。まだ見えてなくて、ご自分で見つけたいという方もいると思いますので、答えをめくるタイミングはお任せします。
今後も良い問題に出会いましたら、更新していくのでたまには遊びに来てください。では、また!
正三角形をいかに作るかということです。この発想がないと、補助線を引こうと考えたとき、大体、ある辺に平行な補助線を引こうとしか考えつかないと思います。私の経験上、角度を求める難問は、多く場合、正三角形が絡んできます。このたった一つの奥義を覚えているだけで、角度を求める難問はかなりの確率で倒せるようになります。(自分がそうでした)
上の第四問は角の二等分線がカギとなりましたが、もしかしたら正三角形を用いて解く方法もあるのかもしれませんね。その辺の研究は皆さんにお任せします。
上の第四問は角の二等分線がカギとなりましたが、もしかしたら正三角形を用いて解く方法もあるのかもしれませんね。その辺の研究は皆さんにお任せします。



コメント