はじめに
第三回に続いて、今回も3問の厳選問題について学んでいこう!
今回は『外積』に関する問題だ。意外と知られていない、目からうろこの計算法があるぞ!
問題.10
次のベクトル \(\boldsymbol{a}、\boldsymbol{b}\) の外積 \(\boldsymbol{a} \times \boldsymbol{b}\) を求めよ。$$\boldsymbol{a}=\left( \begin{array}{c}1\\3\\2 \end{array} \right)、\boldsymbol{b}=\left( \begin{array}{c}2\\-2\\1 \end{array} \right)$$
問題.11
空間内の原点 \(O\) と三点 \(A(1 , 3 , 2)、B(2 , -2 , 1)、C(-2 , 1 , 1)\) を頂点にもつ平行六面体の体積を求めよ。\(\boldsymbol{a}=(1 , 3 , 2)\)、\(\boldsymbol{b}=(2 , -2 , 1)\)、\(\boldsymbol{c}=(-2 , 1 , 1)\) とおくとき、問題の平行六面体とは下図のようになる。
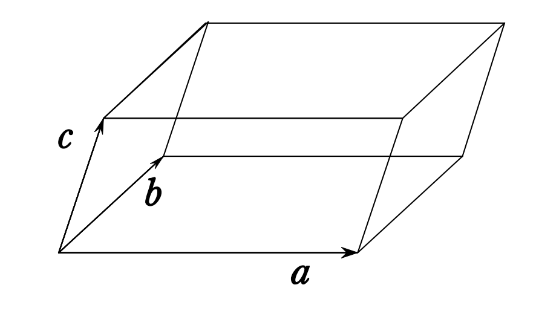
問題.12
空間内で同一直線上にない3点\(P_0(x_0 , y_0 , z_0)、P_1(x_1 , y_1 , z_1)、P_2(x_2 , y_2 , z_2)\) を含む平面の方程式は、
$$\begin{vmatrix}
x&y&z&1\\x_0&y_0&z_0&1\\x_1&y_1&z_1&1\\x_2&y_2&z_2&1
\end{vmatrix}=0$$
で表されることを示せ。
最後に
今回は問題自体はとてもシンプルでだが、その中身はとても含蓄があるものばかりだ。
ぜひ、解説を読んでほしい。そこには問題を解くためだけの知識のみならず、深い理論的な内容も含まれているぞ。
解説にも書いたが、最初のうちは問題を解くことを楽しみながらやり、慣れてきたら徐々に深い内容にも手を付けて行けばよいだろう。
長く続けることが一番大切だということを忘れないでほしい。ではまた!




コメント