第十二回 解答
問題.34 解答
(1)の解答の前に
(1)は実対称行列 \(A\) (\({}^{t}\!A=A\))の固有値と固有ベクトルに関する問題だ。本問で問われている性質は、問題.35と問題.36で問われている『2次形式』に関する問題を解く上で非常に大切になるものだ。
実対称行列の固有値は実数になることを示すのであるが、与えられた行列は \(n\) 次であるから、固有方程式:\(|\lambda E-A|=0\) は \(\lambda\) に関する \(n\) 次方程式になる。2次方程式ならば、判別式を用いて二つの解が実数であるか否かを判定できるが、\(n\) 次方程式の判別式など知らない。一体どうやるのだろう? というのがこの問題の難しさである。
結論を言うと、『内積』を用いて示すのだ! このことはなかなか思いつかないことなのでしっかり覚えておきたいところだ。
(1)の解答
(1) (証明)
\(\lambda\ \in\ \mathbb{C}\) を \(A\) の任意の固有値とし、\(\lambda\) に属する固有ベクトルの一つを \(\boldsymbol{v}\ne \boldsymbol{0}\) とする。
このとき、エルミート内積 \((\cdot\ ,\ \cdot)\) に対して、
$$(A\boldsymbol{v} , \boldsymbol{v})=(\lambda\boldsymbol{v} , \boldsymbol{v})=\lambda(\boldsymbol{v} , \boldsymbol{v})=\lambda\|\boldsymbol{v}\|^{2}\ \cdots\ ①$$
一方、エルミート内積に対して、\((A\boldsymbol{v} , \boldsymbol{v})=(\boldsymbol{v} , A^{\ast}\boldsymbol{v})\) が成り立つので、
$$(A\boldsymbol{v} , \boldsymbol{v})=(\boldsymbol{v} , A^{\ast}\boldsymbol{v})=(\boldsymbol{v} , {}^{t}\!(\overline{A})\boldsymbol{v})=(\boldsymbol{v} , A\boldsymbol{v})=(\boldsymbol{v} , \lambda\boldsymbol{v})=\overline{\lambda}(\boldsymbol{v} , \boldsymbol{v})=\overline{\lambda}\|\boldsymbol{v}\|^{2}\ \cdots\ ②$$
①、②より、
$$\lambda\|\boldsymbol{v}\|^{2}=\overline{\lambda}\|\boldsymbol{v}\|^{2} \Longleftrightarrow \lambda=\overline{\lambda} \Longleftrightarrow \lambda \in \mathbb{R}.$$
したがって、\(A\) の任意の固有値の \(\lambda\) は実数である。
(1)の後半について
次に、異なる固有値 \(\lambda_1、\lambda_2\) に属する固有ベクトルをそれぞれ \(\boldsymbol{v}_1、\boldsymbol{v}_2\) とすると、
$$(A\boldsymbol{v}_1 , \boldsymbol{v}_2)=(\lambda_1\boldsymbol{v}_1 , \boldsymbol{v}_2)=\lambda_1(\boldsymbol{v}_1 , \boldsymbol{v}_2)\ \cdots\ ③$$
また、
$$(A\boldsymbol{v}_1 , \boldsymbol{v}_2)=(\boldsymbol{v}_1 , A^{\ast}\boldsymbol{v}_2)=(\boldsymbol{v}_1 , A\boldsymbol{v}_2)=(\boldsymbol{v}_1 , \lambda_2\boldsymbol{v}_2)=\overline{\lambda_2}(\boldsymbol{v}_1 , \boldsymbol{v}_2)=\lambda_2(\boldsymbol{v}_1 , \boldsymbol{v}_2)\ \cdots\ ④$$
※前半で示したことにより、\(\lambda_2 \in \mathbb{R}\) より、\(\overline{\lambda_2}=\lambda_2\)
③、④より、
$$\lambda_1(\boldsymbol{v}_1 , \boldsymbol{v}_2)=\lambda_2(\boldsymbol{v}_1 , \boldsymbol{v}_2) \Longleftrightarrow (\lambda_1-\lambda_2)(\boldsymbol{v}_1 , \boldsymbol{v}_2)=0 \Longleftrightarrow (\boldsymbol{v}_1 , \boldsymbol{v}_2)=0$$
したがって、\(\boldsymbol{v}_1と\boldsymbol{v}_2\) は直交する。 (\(q.e.d.\))
(2)の解答の前に
(2)は実交代行列 \(B\) (\({}^{t}\!B=-B\)) の固有値と対角化に関する問題だ。
固有値が0または純虚数になることは(1)と同様に内積を用いてできる。
そして、後半の交代行列が対角化可能であることの証明は、前回の問題で取り扱った『行列の三角化』を利用するぞ。(復習はこちらから)
(2)の解答
(証明)
\(\beta\ \in\ \mathbb{C}\) を \(B\) の任意の固有値とし、\(\beta\) に属する固有ベクトルの一つを \(\boldsymbol{w}\ne \boldsymbol{0}\) とする。
このとき、エルミート内積 \((\cdot\ ,\ \cdot)\) に対して、
$$(B\boldsymbol{w} , \boldsymbol{w})=(\beta\boldsymbol{w} , \boldsymbol{w})=\beta(\boldsymbol{w} , \boldsymbol{w})=\beta\|\boldsymbol{w}\|^{2}\ \cdots\ ①$$
一方、エルミート内積に対して、\((B\boldsymbol{w} , \boldsymbol{w})=(\boldsymbol{w} , B^{\ast}\boldsymbol{w})\) が成り立つので、
$$(B\boldsymbol{w} , \boldsymbol{w})=(\boldsymbol{w} , B^{\ast}\boldsymbol{w})=(\boldsymbol{w} , {}^{t}\!(\overline{B})\boldsymbol{w})$$
$$=(\boldsymbol{w} , -B\boldsymbol{w})=(\boldsymbol{w} , -\beta\boldsymbol{w})=-\overline{\beta}(\boldsymbol{w} , \boldsymbol{w})=-\overline{\beta}\|\boldsymbol{w}\|^{2}\ \cdots\ ②$$
①、②より、
$$\beta\|\boldsymbol{w}\|^{2}=-\overline{\beta}\|\boldsymbol{w}\|^{2} \Longleftrightarrow (\beta+\overline{\beta})\|\boldsymbol{w}\|^{2} \Longleftrightarrow \beta+\overline{\beta}=0 \Longleftrightarrow \beta=0または純虚数.$$
したがって、交代行列 \(B\) の固有値は \(0\) 、または純虚数である。
(2)の後半について
第11回の問題.33の解答で紹介した定理 \(\spadesuit\) により、
あるユニタリ行列 \(Q\) が存在して、
$$Q^{-1}BQ=\begin{pmatrix} \beta_1 \\ & \beta_2 & & \huge{\ast} \\ & & \ddots \\ & \huge{0} & & \ddots \\ & & & & \beta_n \end{pmatrix}$$
と三角化される。ここで、\(Q\) はユニタリ行列で、\(Q^{\ast}=Q^{-1}\) を満たすので、
$$(Q^{-1}BQ)^{\ast}=Q^{\ast}B^{\ast}(Q^{-1})^{\ast}=(Q^{-1}){}^{t}\!(\overline{B})Q=Q^{-1}(-B)Q=-(Q^{-1}BQ)$$
すなわち、\((Q^{-1}BQ)^{\ast}=-(Q^{-1}BQ)\) を得る。これは、
$$\begin{pmatrix} \overline{\beta_1} \\ & \overline{\beta_2} & & \huge{0} \\ & & \ddots \\ & \huge{\ast} & & \ddots \\ & & & & \overline{\beta_n} \end{pmatrix}=\begin{pmatrix} -\beta_1 \\ & -\beta_2 & & -\huge{\ast} \\ & & \ddots \\ & \huge{0} & & \ddots \\ & & & & -\beta_n \end{pmatrix}$$
が成り立つことを意味する。
これより、\(\ast\) に属する成分はすべて \(0\) となることが分かる。
つまり、\(B\) を三角化する行列 \(Q\) は、実は \(B\) を対角化する行列だったのだ。
以上により、実交代行列は対角化可能である。 (\(q.e.d.\))
※上とまったく同様に、『実対称行列』もある直交行列 \(P\) によって対角化可能であることも示される。
・実対称行列の固有値は実数であり、実交代行列の固有値は \(0\) または純虚数である。
・実対称行列と、実交代行列は対角化可能である。
問題.35 解答
(1)の解答の前に
本問は『2次形式』に関する基本的な問題だ。2次形式とは、高校で習う2次曲線、つまり放物線や楕円や双曲線などを扱う分野と密接な関係がある。次の問題.36でその応用を見るだろう。
はじめに、2次曲線がどういうものなのかをしっかり理解しておかなければなるまい。
2次形式の定義
\(n\) 個の変数 \(x_1、x_2、\cdots、x_n\) に関する実係数の2次の同次多項式:
$$d(x_1 , \cdots , x_n)=\sum_{i , j=1}^{n}c_{ij}x_ix_j\ (c_{ij}\ \in\ \mathbb{R})\ \cdots\ \star$$
を(\(n\)変数)実2次形式という。
ここで、2次の同次多項式とは、各項の次数がすべて2次であるような多項式のことである。例えば、
$$x_1^{2}+x_2^{2}\ ,\\ \ \ x_1^{2}+2x_1x_2+3x_2x_3\ ,\\ \ \ x_1^{2}+x_2^{2}+x_3^{2}+2x_1x_2-2x_2x_3-2x_1x_3$$
などはすべて実2次形式である。
さて、\(\star\) において \(n=2\) とすると、
$$d(x_1 , x_2)=\sum_{i , j=1}^{2}c_{ij}x_ix_j$$
$$=c_{11}x_1x_1+c_{12}x_1x_2+c_{21}x_2x_1+c_{22}x_2x_2$$
$$=c_{11}x_1^{2}+(c_{12}+c_{21})x_1x_2+c_{22}x_2^{2}$$
と書ける。(つまり、同類項をまとめたということ)
そして、\(a_{12}\ \stackrel{\mathrm{def}}{=}\ \frac{c_{12}+c_{21}}{2}\) とおくと、当然、\(a_{12}=a_{21}\)が成り立ち、
$$d(x_1 , x_2)=\sum_{i , j=1}^{2}c_{ij}x_ix_j=a_{11}x_1^{2}+2a_{12}x_1x_2+a_{22}x_2^{2}$$
を得る。そして右辺について、行列を用いて書き直すと、
$$a_{11}x_1^{2}+2a_{12}x_1x_2+a_{22}x_2^{2}=(x_1 , x_2)\begin{pmatrix}a_{11}&a_{12}\\a_{12}&a_{22}\end{pmatrix}\begin{pmatrix}x_1\\x_2\end{pmatrix}={}^{t}\!\boldsymbol{x}A\boldsymbol{x}$$
となる。ただし、
$$\boldsymbol{x}=\begin{pmatrix}x_1\\x_2\end{pmatrix}\ ,\ A=\begin{pmatrix}a_{11}&a_{12}\\a_{12}&a_{22}\end{pmatrix}$$
とおいた。実際に右辺を計算すると、
$$(x_1 , x_2)\begin{pmatrix}a_{11}&a_{12}\\a_{12}&a_{22}\end{pmatrix}\begin{pmatrix}x_1\\x_2\end{pmatrix}$$
$$=(a_{11}x_1+a_{12}x_2 \ ,\ a_{12}x_1+a_{22}x_2)\begin{pmatrix}x_1\\x_2\end{pmatrix}$$
$$=(a_{11}x_1+a_{12}x_2)x_1+(a_{12}x_1+a_{22}x_2)x_2$$
$$=a_{11}x_1^{2}+2a_{12}x_1x_2+a_{22}x_2^{2}$$
となって、確かに成り立つことが分かる。
今は、\(n=2\) の場合を考えたが、同様の計算は \(n\) 変数の場合もできて、その場合も、
$$d(x_1 , \cdots , x_n)=\sum_{i , j=1}^{n}c_{ij}x_ix_j={}^{t}\!\boldsymbol{x}A\boldsymbol{x}$$
と書ける。ただし、\(a_{ij}\ \stackrel{\mathrm{def}}{=}\ \frac{c_{ij}+c_{ji}}{2}\) の下、
$$\boldsymbol{x}=\begin{pmatrix}x_1\\ \vdots\\ x_n\end{pmatrix}\ ,\ A=\begin{pmatrix}a_{11}& \cdots &a_{1n}\\ \vdots& \ddots & \vdots\\a_{1n}& \cdots&a_{nn}\end{pmatrix}$$
とおいた。
つまり、何が言いたいかというと、どんな2次形式も行列を用いて、
$$d(x_1 , \cdots , x_n)={}^{t}\!\boldsymbol{x}A\boldsymbol{x}$$
と書けるということだ。このように書いたとき、右辺の行列 \(A\) を
『2次形式 \(d(x_1 , \cdots , x_n)\) の行列』という。ついでに言えば、
\(n\) 変数の実2次形式全体を \(D_n(\mathbb{R})\) 、\(n\) 次実対称行列全体を \(TM_n(\mathbb{R})\) と表すと、
$$D_n(\mathbb{R})\ \longrightarrow \ TM_n(\mathbb{R})\ \stackrel{\mathrm{def}}{\Leftrightarrow}\ d(\boldsymbol{x})\ \longrightarrow \ A$$
なる対応によって \(1:1\) に対応することを伝えておきたい。
以上が2次形式についての基礎知識である。
(1)の解答
与えられた2次形式を行列表示に直すには、一つの文字で2次となっている項、つまり、\(x_1^{2}\ ,\ x_2^{2}\ ,\ x_3^{2}\) 以外の項を2でくくることから始める。今回そのような項は、\(-2x_1x_3\) の一つしかないが、あえてカッコでくくって強調すると、
$$d(x_1 , x_2 , x_3)=x_1^{2}+x_2^{2}+x_3^{2}+2(-x_1x_3)$$
すると、2でくくられた後の \(x_1x_3\) の係数は \(-1\) であるから、これは \(3 \times 3\) 行列の \((1 , 3)\) 成分と \((3 , 1)\) 成分が \(-1\) であることを意味する。
そして、\(x_1^{2}\ ,\ x_2^{2}\ ,\ x_3^{2}\) の係数が対角成分になるので、対角線分はすべて \(1\) である。触れなかった他の成分はすべて \(0\) となる。したがって、
$$d(x_1 , x_2 , x_3)=x_1^{2}+x_2^{2}+x_3^{2}+2(-x_1x_3)=(x_1 , x_2 , x_3)\begin{pmatrix}1&0&-1\\0&1&0\\-1&0&1\end{pmatrix}\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}$$
と書ける。ゆえに、求める『2次形式の行列』は、
$$A=\begin{pmatrix}1&0&-1\\0&1&0\\-1&0&1\end{pmatrix}\ \cdots\ (答)$$
(2)の解答の前に
(2)は2次形式の標準形を求める問題である。この問題は2次形式関連の問題の中で中核をなすものである。これ以上ないくらい丁寧に説明するので、最後の山場だと思ってじっくり考えて進んでほしい。
この問題の解答は、次の定理(主軸定理)を根拠としている。
主軸定理
実2次形式:\(d(\boldsymbol{x})={}^{t}\!\boldsymbol{x}A\boldsymbol{x}\) は、適当な直交行列 \(P\) による変数変換: \(\boldsymbol{x}=P\boldsymbol{x’}\) によって、
$$d(\boldsymbol{x})={}^{t}\!\boldsymbol{x}A\boldsymbol{x}={}^{t}\!\boldsymbol{x’}({}^{t}\!PAP)\boldsymbol{x’}=\lambda_1(x_1^{\prime})^{2}+\cdots+\lambda_n(x_n^{\prime})^{2}$$
の形(標準形)に変換される。(この変換を主軸変換ともいう)
ここで、\(\lambda_i\ (1 \le i \le n)\) は \(A\) の固有値である。
以下、この定理を詳しく掘り下げていこう!
変数変換と基底の変換が同じこと
まず、与えられた2次形式:\(d(\boldsymbol{x})={}^{t}\!\boldsymbol{x}A\boldsymbol{x}\) に変数変換: \(\boldsymbol{x}=P\boldsymbol{x’}\ \cdots\ ①\)
をするということは、
基底の変換: \(\{\boldsymbol{e}_i\} \stackrel{P}{\longrightarrow}\{\boldsymbol{p}_i\} \) を行うことと同じであることに注意する。すなわち、
$$(\boldsymbol{p}_1 , \cdots , \boldsymbol{p}_n)=(\boldsymbol{e}_1 , \cdots , \boldsymbol{e}_n)P$$
なる変換である。
なぜこのような注意をするかというと、問題によっては『変数変換』の部分を、『基底の変換』と表現している問題もあるかもしれないからだ。どちらも同じことを言っているのに、同じだということを知らないと、場合によっては詰まってしまう恐れがあるのだ。やるからには完璧を目指そう!
さて、このように基底を変換したとき、一般の変数ベクトル \(\boldsymbol{x}={}^{t}\!(x_1 , \cdots , x_n)\) が、新しい基底:\(\{\boldsymbol{p}_1 , \cdots , \boldsymbol{p}_n\}\) を用いて、
$$(\boldsymbol{x}=)\sum_{i-1}^{n}x_i\boldsymbol{e}_i=\sum_{i-1}^{n}x_i^{\prime}\boldsymbol{p}_i$$
と表されたとしよう。この両辺は、
$$(\boldsymbol{e}_1 , \cdots , \boldsymbol{e}_n)\boldsymbol{x}=(\boldsymbol{p}_1 , \cdots , \boldsymbol{p}_n)\boldsymbol{x’}$$
$$\Leftrightarrow (\boldsymbol{e}_1 , \cdots , \boldsymbol{e}_n)\boldsymbol{x}=((\boldsymbol{e}_1 , \cdots , \boldsymbol{e}_n)P)\boldsymbol{x’}$$
$$\Leftrightarrow (\boldsymbol{e}_1 , \cdots , \boldsymbol{e}_n)\boldsymbol{x}=(\boldsymbol{e}_1 , \cdots , \boldsymbol{e}_n)(P\boldsymbol{x’})$$
と変形される。\(\{\boldsymbol{e}_1 , \cdots , \boldsymbol{e}_n\}\) は1次独立であるから、これより、
$$\boldsymbol{x}=P\boldsymbol{x’}$$
を得る。これは、①に一致する。
これで、基底の変換: \(\{\boldsymbol{e}_i\} \stackrel{P}{\longrightarrow}\{\boldsymbol{p}_i\} \) を行うことは、変数変換: \(\boldsymbol{x}=P\boldsymbol{x’}\)を行うことと同じであることが分かった。
変数変換後の2次形式
さて、2次形式:\(d(\boldsymbol{x})={}^{t}\!\boldsymbol{x}A\boldsymbol{x}\) に変数変換: \(\boldsymbol{x}=P\boldsymbol{x’}、\)
あるいは基底の変換: \(\{\boldsymbol{e}_i\} \stackrel{P}{\longrightarrow}\{\boldsymbol{p}_i\} \) を行うと、
$$d(\boldsymbol{x})={}^{t}\!\boldsymbol{x}A\boldsymbol{x}={}^{t}\!(P\boldsymbol{x’})A(P\boldsymbol{x’})={}^{t}\!\boldsymbol{x’}{}^{t}\!PAP\boldsymbol{x’}={}^{t}\!\boldsymbol{x’}({}^{t}\!PAP)\boldsymbol{x’}$$
と書けるだろう。ここで、
$${}^{t}\!({}^{t}\!PAP)={}^{t}\!P{}^{t}\!AP={}^{t}\!PAP$$
が成り立つので、\({}^{t}\!PAP\) は実対称行列であることに注意する。
これは、\(\boldsymbol{x}={}^{t}(x_1 , \cdots , x_n)\) についての2次形式:
$$d(\boldsymbol{x})={}^{t}\!\boldsymbol{x}A\boldsymbol{x}$$
が、\(\boldsymbol{x’}={}^{t}(x_1^{\prime} , \cdots , x_n^{\prime})\) についての2次形式:
$$d(\boldsymbol{x})={}^{t}\!\boldsymbol{x’}({}^{t}\!PAP)\boldsymbol{x’}$$
に書き換えられたことを意味する。
これで、『主軸定理』を証明する準備が整ったのでこれから証明しよう。
主軸定理の証明
実2次形式:\(d(\boldsymbol{x})={}^{t}\!\boldsymbol{x}A\boldsymbol{x}\) は、適当な直交行列 \(P\) による変数変換: \(\boldsymbol{x}=P\boldsymbol{x’}\) によって、
$$d(\boldsymbol{x})={}^{t}\!\boldsymbol{x}A\boldsymbol{x}={}^{t}\!\boldsymbol{x’}({}^{t}\!PAP)\boldsymbol{x’}=\lambda_1(x_1^{\prime})^{2}+\cdots+\lambda_n(x_n^{\prime})^{2}$$
の形(標準形)に変換される。(この変換を主軸変換ともいう)
ここで、\(\lambda_i\ (1 \le i \le n)\) は \(A\) の固有値である。
(1)で求めた \(A\) は実対称行列なので、問題.34の(2)の後半の解答で紹介した通り、ある直交行列 \(P\) によって対角化される。すなわち、
$$P^{-1}AP=\begin{pmatrix} \lambda_1 \\ & \lambda_2 & & \huge{0} \\ & & \ddots \\ & \huge{0} & & \ddots \\ & & & & \lambda_n \end{pmatrix}$$
とできる。
この直交行列 \(P\) を用いて、変数変換: \(\boldsymbol{x}=P\boldsymbol{x’}\) を行うのだ!(←ここがポイント!)
すると上で見たように2次形式は、
$$d(\boldsymbol{x})={}^{t}\!\boldsymbol{x’}({}^{t}\!PAP)\boldsymbol{x’}$$
と書き直される。
\(P\) は直交行列だから、\({}^{t}\!PP=P{}^{t}\!P=E\) すなわち、\({}^{t}\!P=P^{-1}\) が成り立つので、上式はさらに、
$$d(\boldsymbol{x})={}^{t}\!\boldsymbol{x’}({}^{t}\!PAP)\boldsymbol{x’}={}^{t}\!\boldsymbol{x’}(P^{-1}AP)\boldsymbol{x’}$$
$$={}^{t}\!\boldsymbol{x’}\begin{pmatrix} \lambda_1 \\ & \lambda_2 & & \huge{0} \\ & & \ddots \\ & \huge{0} & & \ddots \\ & & & & \lambda_n \end{pmatrix}\boldsymbol{x’}=\sum_{i=1}^{n}\lambda_i(x_i^{\prime})^{2}$$
と書ける。これは、主軸定理が主張していた結論である。 \(q.e.d.\)
要は、与えられた2次形式の標準形を求めるためには、(1)で求めたように『2次形式の行列 \(A\) 』を求め、それを対角化するための直交行列 \(P\) を求めるということになる。そして、求めた \(P\) をつかって与えられた2次形式を変数変換すれば終わりというわけだ。
要するに実対称行列を対角化することが本質であったのだ!
では、(2)の解答に移ろう。
(2)の解答
(1)で『2次形式の行列』を求めた。いま一度書くと、
$$A=\begin{pmatrix}1&0&-1\\0&1&0\\-1&0&1\end{pmatrix}$$
である。まずは、この行列を直交行列を用いて対角化するのであった。そのために固有方程式を解く。
$$|\lambda E-A|=0 \Leftrightarrow \begin{vmatrix}\lambda-1&0&1\\0&\lambda-1&0\\1&0&\lambda-1\end{vmatrix}=0$$
$$\Leftrightarrow (\lambda-1)^{3}-(\lambda-1)=0 \Leftrightarrow \lambda(\lambda-1)(\lambda-2)=0$$
よって、固有値は \(\lambda=0 , 1 , 2\) となる。
次に固有ベクトルを求める。
(\(\lambda=0\) のとき)
$$\begin{pmatrix}-1&0&1\\0&-1&0\\1&0&-1\end{pmatrix}\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=\begin{pmatrix}0\\0\\0\end{pmatrix}$$
$$\Leftrightarrow \begin{cases}x_1=x_3\\x_2=0\end{cases}$$
$$\Leftrightarrow \begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=c\begin{pmatrix}1\\0\\1\end{pmatrix}\ (c\ \in\ \mathbb{R}\ (or\ \mathbb{C}))$$
よって、\(\lambda=0\) に属する固有ベクトルとして、\(\boldsymbol{q}_1=\begin{pmatrix}1\\0\\1\end{pmatrix}\) を得る。
(\(\lambda=1\) のとき)
$$\begin{pmatrix}0&0&1\\0&0&0\\1&0&0\end{pmatrix}\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=\begin{pmatrix}0\\0\\0\end{pmatrix}$$
$$\Leftrightarrow \begin{cases}x_1=x_3=0\\x_2:任意\end{cases}$$
$$\Leftrightarrow \begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=c\begin{pmatrix}0\\1\\0\end{pmatrix}\ (c\ \in\ \mathbb{R}\ (or\ \mathbb{C}))$$
よって、\(\lambda=1\) に属する固有ベクトルとして、\(\boldsymbol{q}_2=\begin{pmatrix}0\\1\\0\end{pmatrix}\) を得る。
(\(\lambda=2\) のとき)
$$\begin{pmatrix}1&0&1\\0&1&0\\1&0&1\end{pmatrix}\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=\begin{pmatrix}0\\0\\0\end{pmatrix}$$
$$\Leftrightarrow \begin{cases}x_1+x_3=0\\x_2=0\end{cases}$$
$$\Leftrightarrow \begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=c\begin{pmatrix}1\\0\\-1\end{pmatrix}\ (c\ \in\ \mathbb{R}\ (or\ \mathbb{C}))$$
よって、\(\lambda=2\) に属する固有ベクトルとして、\(\boldsymbol{q}_3=\begin{pmatrix}1\\0\\-1\end{pmatrix}\) を得る。
これで、固有ベクトルを全て求めた。次に、これら固有ベクトルから直交行列を作るため、各固有ベクトルの長さを \(1\) にすればよい。
シュミットの直交化法を使わなくてよいのかと思うかもしれないが、うれしいことにそこまでする必要はない。それは前問の問題.34の(1)から、『\(A\) が対称行列 (\({}^{t}\!A=A\)) のとき、\(A\) の固有値はすべて実数であり、かつ異なる固有値に対する固有ベクトルは直交する』からである。
上で求めた固有ベクトル \(\boldsymbol{q}_1\ ,\ \boldsymbol{q}_2\ ,\ \boldsymbol{q}_3\) は異なる固有値から求めたので、これらの直交性は保証されているのだ。
さて、\(\{\boldsymbol{q}_1\ ,\ \boldsymbol{q}_2\ ,\ \boldsymbol{q}_3\}\) の長さを \(1\) にしてできる正規直交基底を \(\{\boldsymbol{p}_1\ ,\ \boldsymbol{p}_2\ ,\ \boldsymbol{p}_3\}\) とおくと、
$$\boldsymbol{p}_1=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\0\\1\end{pmatrix}\ ,\ \boldsymbol{p}_2=\begin{pmatrix}0\\1\\0\end{pmatrix}\ ,\ \boldsymbol{p}_3=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\0\\-1\end{pmatrix}$$
となる。ここで、直交行列 \(P\) を
$$P=(\boldsymbol{p}_1\ ,\ \boldsymbol{p}_2\ ,\ \boldsymbol{p}_3)=\begin{pmatrix}\frac{1}{\sqrt{2}}&0&\frac{1}{\sqrt{2}}\\0&1&0\\\frac{1}{\sqrt{2}}&0&-\frac{1}{\sqrt{2}}\end{pmatrix}$$
と定めると、行列 \(A\) は、
$$P^{-1}AP=\begin{pmatrix}0&0&0\\0&1&0\\0&0&2\end{pmatrix}$$
と対角化される。これで、対角化するための直交行列がえられたので、次にやることはこの直交行列 \(P\) を用いて変数変換: \(\boldsymbol{x}=P\boldsymbol{x’}\) をすることだ。すると、
$$d(\boldsymbol{x})=d(x_1 , x_2 , x_3)={}^{t}\boldsymbol{x}A\boldsymbol{x}={}^{t}\!\boldsymbol{x’}({}^{t}\!PAP)\boldsymbol{x’}={}^{t}\!\boldsymbol{x’}(P^{-1}AP)\boldsymbol{x’}$$
$$=(x_1^{\prime} , x_2^{\prime} , x_3^{\prime})\begin{pmatrix}0&0&0\\0&1&0\\0&0&2\end{pmatrix}\begin{pmatrix}x_1^{\prime}\\x_2^{\prime}\\x_3^{\prime}\end{pmatrix}=(x_2^{\prime})^{2}+2(x_3^{\prime})^{2}\ \cdots\ (答)$$
と標準形に変換される。
※因みに上で正規直交基底 \(\{\boldsymbol{p}_1\ ,\ \boldsymbol{p}_2\ ,\ \boldsymbol{p}_3\}\) を主軸という。
以上が、主軸変換のやり方である。この応用は、次の問題(ラスト1問)で見ることになるだろう。
問題.36 解答
解答の前に
本問は、前問で行った主軸変換を『2次曲線』へ応用する問題である。
与えられた2次曲線は、\(C : f(x , y)=2x^{2}+2xy+2y^{2}=3\) である。これは高校数学で学んだ2次曲線(放物線、楕円、双曲線)のどれなのかこのままでは分からない。
おそらく、これらのうちどれかが、回転や平行移動したものなのだろうという予想が立てば、非常に鋭い直感をしているぞ!
実は、それを教えてくれるのが前問で見た『主軸変換』なのだ。
与えられた2次曲線 \(C : 2x^{2}+2xy+2y^{2}=3\) をもう一度見てみよう。
左辺の \(f(x , y)=2x^{2}+2xy+2y^{2}\) 正に『2次形式』になっているだろう。
まず、この左辺を主軸変換することから始めるぞ!
問題.36の解答
\(f(x , y)=2x^{2}+2xy+2y^{2}=2x^{2}+2y^{2}+2xy\) は2変数の2次形式である。
行列表示に直すと、
$$f(x , y)=2x^{2}+2y^{2}+2xy=(x , y)\begin{pmatrix}2&1\\1&2\end{pmatrix}\begin{pmatrix}x\\y \end{pmatrix}$$
となる。\(A=\begin{pmatrix}2&1\\1&2\end{pmatrix}\) とおく。
\(A\) の固有値を求める。
$$|\lambda E-A|=0 \Longleftrightarrow \begin{vmatrix}\lambda-2&-1\\-1&\lambda-2\end{vmatrix}=0 \Longleftrightarrow (\lambda-2)^{2}-1=0 \Longleftrightarrow \lambda=2\pm1$$
したがって、固有値 \(\lambda=1 , 3\) を得る。
固有ベクトル求める。
(\(\lambda=1\) のとき)
$$\begin{pmatrix}-1&-1\\-1&-1\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}0\\0 \end{pmatrix} \Longleftrightarrow x+y=0$$
よって、\(\begin{pmatrix}x\\y\end{pmatrix}=c\begin{pmatrix}1\\-1\end{pmatrix}\ (c\ \in\ \mathbb{R}\ (or\ \mathbb{C}))\) となる。
したがって、\(\lambda=1\) に属する固有ベクトルとして、\(\boldsymbol{x}=\begin{pmatrix}1\\-1\end{pmatrix}\) を得る。
(\(\lambda=3\) のとき)
$$\begin{pmatrix}1&-1\\-1&1\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}0\\0 \end{pmatrix} \Longleftrightarrow x-y=0$$
よって、\(\begin{pmatrix}x\\y\end{pmatrix}=c\begin{pmatrix}1\\1\end{pmatrix}\ (c\ \in\ \mathbb{R}\ (or\ \mathbb{C}))\) となる。
したがって、\(\lambda=3\) に属する固有ベクトルとして、\(\boldsymbol{x}=\begin{pmatrix}1\\1\end{pmatrix}\) を得る。
次に直交行列を作るため、上で得た固有ベクトルを正規化する。
$$\boldsymbol{p}_1=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\-1\end{pmatrix}\ ,\ \boldsymbol{p}_2=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\1\end{pmatrix}$$
とおいて、直交行列 \(P\) を
$$P=(\boldsymbol{p}_1 , \boldsymbol{p}_2)=\begin{pmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{pmatrix} $$
と定める。次に、この直交行列を使って変数変換:\(\begin{pmatrix}x\\y\end{pmatrix}=P\begin{pmatrix}x’\\y’\end{pmatrix}\) を行う。
すると、
$$f(x , y)=2x^{2}+2y^{2}+2xy=(x , y)\begin{pmatrix}2&1\\1&2\end{pmatrix}\begin{pmatrix}x\\y \end{pmatrix}$$
$$=(x , y)A\begin{pmatrix}x\\y \end{pmatrix}$$
$$=(x’ , y’)({}^{t}\!PAP)\begin{pmatrix}x’\\y’ \end{pmatrix}$$
$$=(x’ , y’)(P^{-1}AP)\begin{pmatrix}x’\\y’ \end{pmatrix}$$
$$=(x’ , y’)\begin{pmatrix}1&0\\0&3\end{pmatrix}\begin{pmatrix}x’\\y’ \end{pmatrix}$$
$$=(x’)^{2}+3(y’)^{2}$$
と主軸変換される。すなわち、
\(C : f(x , y)=2x^{2}+2xy+2y^{2}=3\) は、変数変換:\(\begin{pmatrix}x\\y\end{pmatrix}=P\begin{pmatrix}x’\\y’\end{pmatrix}\) によって、\((x’)^{2}+3(y’)^{2}=3\) と書けることが分かった。
さて、これは両辺3で割って、
$$\frac{(x’)^{2}}{3}+(y’)^{2}=1$$
となるから、『(横長)楕円』だということが分かる。しかし、どのような楕円かはっきりさせたい。
それを知るためには、前問の『変数変換と基底の変換が同じこと』の理解が必要となる。
(復習はこちら)
つまり、変数変換:
$$\begin{pmatrix}x\\y\end{pmatrix}=P\begin{pmatrix}x’\\y’\end{pmatrix}$$
をすることは、基底の変換:
$$\{\boldsymbol{e}_i\} \stackrel{P}{\longrightarrow}\{\boldsymbol{p}_i\}$$
を行うことと同じであった。ここで、新しい基底 \(\{\boldsymbol{p}_1 , \boldsymbol{p}_2\}\) は、
$$\boldsymbol{p}_1=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\-1\end{pmatrix}\ ,\ \boldsymbol{p}_2=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\1\end{pmatrix}$$
であるから、それぞれ、\(y=-x\ ,\ y=x\) 上のベクトルである。
もともと、\(x\) 軸、\(y\) 軸上の正規直交基底であった \(\{\boldsymbol{e}_1\ ,\ \boldsymbol{e}_2\}\) が、 \(y=-x\ ,\ y=x\) 上の正規直交基底 \(\{\boldsymbol{p}_1\ ,\ \boldsymbol{p}_2\}\) に移されたということは、つまり、この直線 \(y=-x\ ,\ y=x\) が変数変換後の新しい『軸』になるのだ。

言い方を変えれば、\(x’\) 軸が直線 \(y=-x\)、\(y’\) 軸が直線 \(y=x\) ということだ。
したがって、楕円
$$\frac{(x’)^{2}}{3}+(y’)^{2}=1$$
は、\(xy\) 座標平面における楕円 \(\frac{x^{2}}{3}+y^{2}=1\)(右図) を、原点を中心に時計回りに \(45^{\circ}\) だけ回転した楕円(右下図)である。
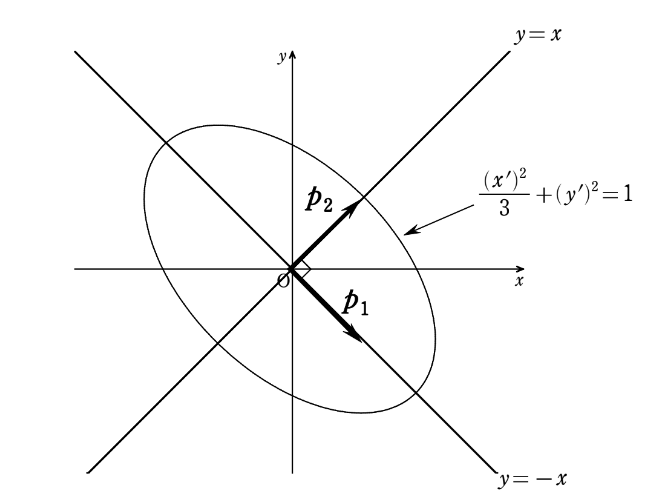
以上により、与えられた2次曲線 \(C : f(x , y)=2x^{2}+2xy+2y^{2}=3\) は \(xy\) 座標平面における楕円 \(\frac{x^{2}}{3}+y^{2}=1\) を、原点を中心に時計回りに \(45^{\circ}\) だけ回転した楕円・・・(答) となる。
最後に
本問をもって、全12回計36問の線形代数の厳選問題を終了する。
大学で学ぶ線形代数の知識を大体において盛り込むように作ったつもりだが、理論的な内容としてはまだまだ薄いというのが真実だ。それでも重要な定理の証明などは与えてきたので、それらが証明まで理解できれば十分だと私は思う。
詳しい理論的な内容はそれなりのテキストを参照してほしい。
第1回の『はじめに』にも書いたことを転記すると、
この記事で一番伝えたいことは、問題を解く上での『タメになる計算テクニック』である。
数学は、まず問題が解けるようにならないと面白さを感じないものである。理論的な内容ばかりを悶々と勉強していても疲れるだけで効果は思ったほどでない。問題を解きながら、必要となれば理論に戻るというスタイルの方が自然だと思う。すべての問題をやり切ったときには確実にスキルアップしているだろう。
ここまでたどり着いた方が、確実にスキルアップしていることを切に願う。 (完)





コメント