与えられた点にフィットする直線とは?

やあ、こんにちは。今日は『単回帰分析』のプログラムを作ってみよう。長くなるので2回に分けてやっていこう。

はい、よろしくお願いします。
『たんかいきぶんせき』と読むのですか?なんだか難しそうですね。

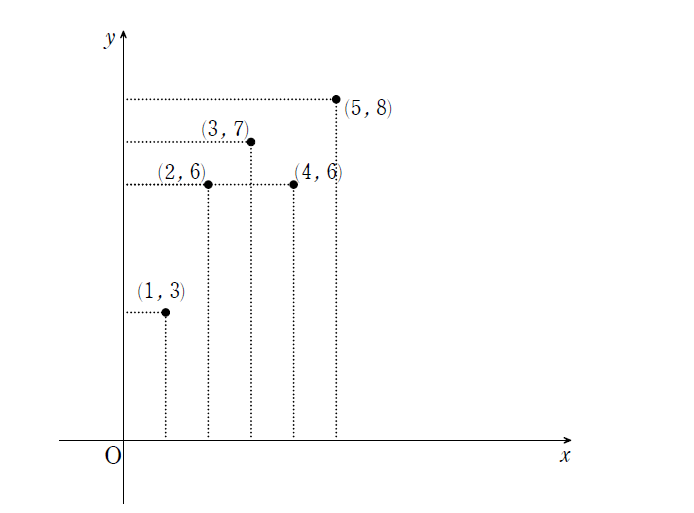
うむ、読みはそれで合ってるぞ。まず単回帰分析がどういうものかを説明しよう。最も簡単に言えば『データに最もフィットする直線を求めること』となる。下の図は5個の点のデータ
$$(1\ ,\ 3)\ ,\ (2\ ,\ 6)\ ,\ (3\ ,\ 7)\ ,\ (4\ ,\ 6)\ ,\ (5\ ,\ 8)$$
を座標平面にとった状態を表している。これら5個の点に最もフィットする直線を考えよう。

先生、フィットするというのはどういう意味なのでしょうか?

いい質問だ。フィットというのは『適当な』や『ふさわしい』という意味の英単語『fit』からきた言葉だ。数学的な厳密な定義を与える前に、フィットしていることを直感的に理解しよう。先ほどの図に直線を2本付け足した下の図を見てほしい。
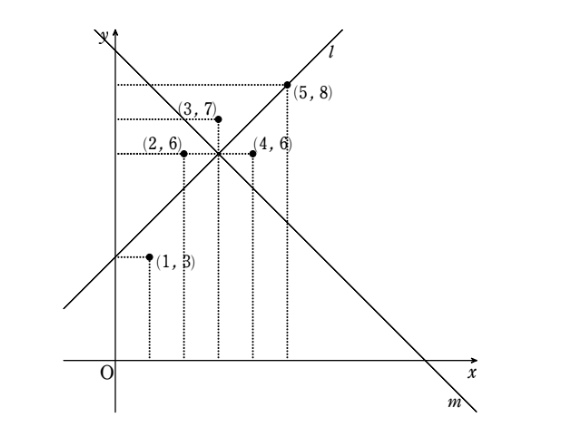

ヒロトは \(l\) と \(m\) のどちらが5個の点に『フィットしている』と思う?

はい、これは明らかに \(l\) の方です。

うむ、それが『フィットしている』ことの直感的な理解だ。では次の場合はどうだ? \(l\) と \(m\) のどちらが5個の点にフィットしていると思う?
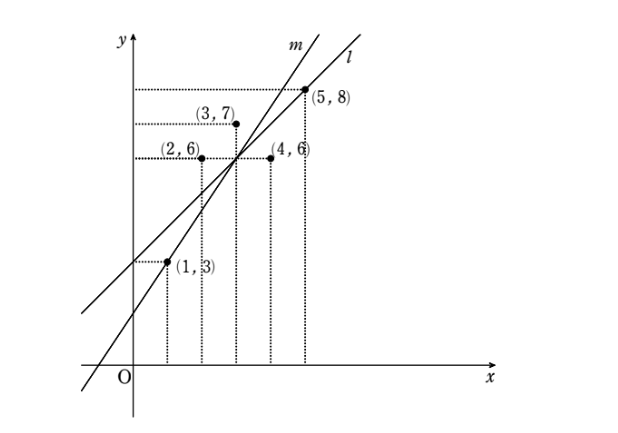

うーん、これはどうだろう?どっちもどっちというのが正直なところですが、どちらか選ばなければならないのなら勘に頼ると思います。
フィットすることの数学的な定義

ふふ、そうだろう?
これが人間の直感の限界なのだ。なので、厳密な数学的な定義が必要となってくる。数学的な定義とは数値的に評価できるものでなければならない。そのために、各点と直線との誤差に注目するのだ。図で説明しよう。
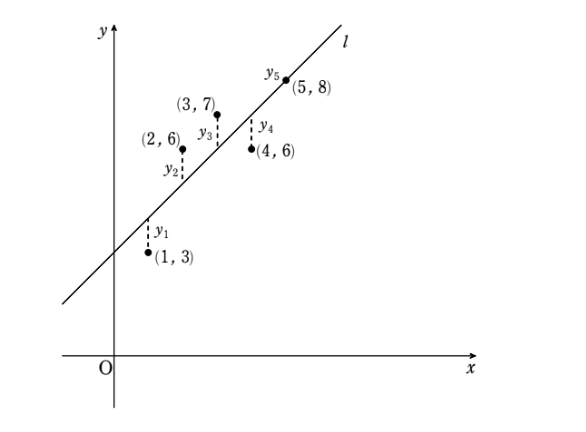

上図のように各点と直線の誤差は、
『\(y\) 座標の値の誤差=点のy座標 ー 直線のyの値』として与えられる。例えば直線が \(l\ :\ y=2x+1\) の場合、各点との誤差を左から順に \(y_1\ ,\ y_2\ ,\ y_3\ ,\ y_4\ ,\ y_5\) とおくと、
\(y_1=3-3=0\ ,\\y_2=6-5=1\ ,\\y_3=7-7=0\ ,\\y_4=6-9=-3\ ,\\y_5=8-11=-3\)
となる。このままだと誤差に正の数と負の数が混ざっていて、別の直線と比較するのが難しくなってしまうので誤差の値をすべて0以上にしたいと考える。さあ、どうすればいいだろうか?

誤差をすべて0以上にするって・・・見当もつきません。

ふふ、意外と単純な方法だぞ。答えは『誤差の2乗を取る』だ。そのうえでそれらの和を取る。つまり、上の例では
$$y_1^{2}+y_2^{2}+y_3^{2}+y_4^{2}+y_5^{2}$$
$$=0^{2}+1^{2}+0^{2}+(-3)^{2}+(-3)^{2}=19$$
これが今回の直線 \(l\ :\ y=2x+1\) と与えられた5個の点の『全体としての誤差の値』と定めるのだ。

なるほど、これで誤差というものが0以上の数として数値化されたというわけですね。

後はこのようにして定めた誤差の値を最小にするような直線を求めることが目標となる。それが、最もフィットする直線ということになるのだ。

つまり、上のように定めた『誤差の2乗和』を最小にする直線、というのが与えられた点にフィットする直線の数学的な定義なのですね!
一般的な直線の場合

さて、今度は一般的な直線 \(l\ :\ y=ax+b\) のついて考えよう。これと与えられた5個の点との誤差の2乗和を求めると、
\(\{3-(a+b)\}^{2}+\{6-(2a+b)\}^{2}+\{7-(3a+b)\}^{2}\\+\{6-(4a+b)\}^{2}+\{8-(5a+b)\}^{2}\)
このままだと \(a\ ,\ b\) が含まれていて見ての通り複雑である。そこでなんとか工夫して \(b\) を消去することを考える。

そんなことできるのですか!
変数を減らすための工夫=中心化

うむ。結論から言えば『平行移動』の考えを使うのだ。
つまり、与えられた5個の点を \((x_i\ ,\ y_i)\ \ (i=1,2,3,4,5)\) とおくとき、
\(x\) 座標と \(y\) 座標の平均 \(\bar{x}\) と \(\bar{y}\) を求め、
新しい5個の点 \((x_i -\bar{x}\ ,\ y_i -\bar{y})\ \ (i=1,2,3,4,5)\) を考えるのだ。
これは、グラフ的には各点を \(x\) 軸方向に \(\bar{x}\)、\(y\) 軸方向に \(\bar{y}\) だけ平行移動することに対応している。

はい、各点が平行移動することは分かります。でも、なぜ平均値の分だけ平行移動すると \(b\) が消去されることになるのですか?

うむ、説明しよう。まずは新しい5個の点の座標を求めてごらん。

はい。まず\(x\) 座標と \(y\) 座標の平均を求めると、
$$\bar{x}=\frac{1+2+3+4+5}{5}=3\ \ ,\ \ \bar{y}=\frac{3+6+7+6+8}{5}=6$$
であるから、新しい5個の点の座標は、
\((1-3\ ,\ 3-6)=(-2\ ,\ -3) ,\\(2-3\ ,\ 6-6)=(-1\ ,\ 0) ,\\(3-3\ ,\ 7-6)=(0\ ,\ 1) ,\\(4-3\ ,\ 6-6)=(1\ ,\ 0) ,\\(5-3\ ,\ 8-6)=(2\ ,\ 2) \)
となります。これらを座標上に表すと下図のようになります。
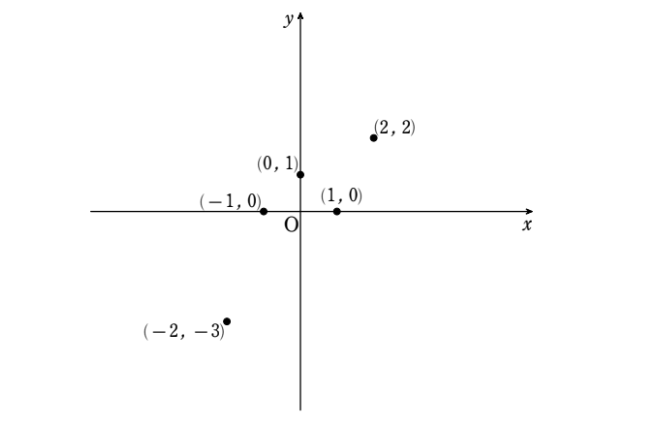

うむ、では次に求めた新しい5個の点の\(x\) 座標と \(y\) 座標の平均を求めてごらん。

はい、まず \(x\) 座標の平均は、
$$\frac{-1-2+0+1+2}{5}=\frac{0}{5}=0$$
次に \(y\) 座標の平均は
$$\frac{-3+0+1+0+2}{5}=\frac{0}{5}=0$$
どちらも0となりました!

その通り。\(x\) 座標と \(y\) 座標の平均が0ということはこれら新しい5個の点に最もフィットする直線は必ず原点を通るものとして考えることができるのだ。つまり、\(y=ax\) の形だ。このように各座標から各平均を引くことを座標の『中心化』というんだ。
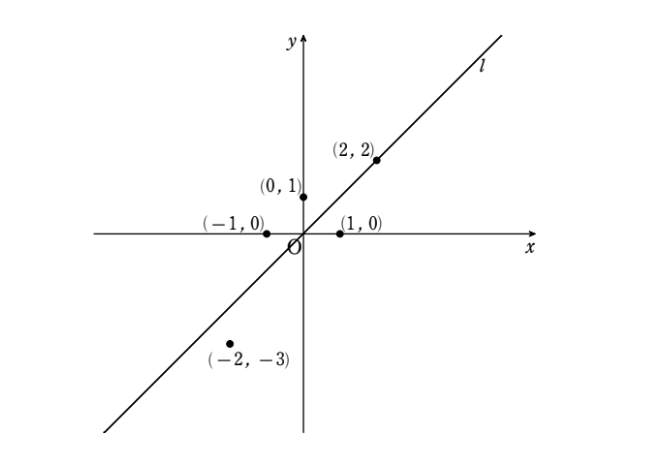

なるほど、こうして \(y\) 切片である \(b\) が消去されるのですね!

うむ、新しい5個の点と、この \(y=ax\) との誤差の2乗和が最小になるような傾き \(a\) だけを求めれば良くなったのだ。そのような \(a\) が求められたならば、あとは直線をもとの位置に平行移動してあげれば本当に求めたかった直線を得られるというわけだ。では実際の計算をやっていこう!
実際の計算

はい、新しい5個の点は先ほど求めた通り
\((-2\ ,\ -3)\ ,\ (-1\ ,\ 0)\ ,\ (0\ ,\ 1)\ ,\ (1\ ,\ 0)\ ,\ (2\ ,\ 2) \) なので、\(y=ax\) との誤差の2乗和は、
$$\{-3-(-2a)\}^{2}+\{0-(-a)\}^{2}+(1-0)^{2}+(0-a)^{2}+(2-2a)^{2}$$
$$=4a^{2}-12a+9+2a^{2}+1+4a^{2}-8a+4$$
$$=10a^{2}-20a+14$$
$$=10\{(a-1)^{2}-1\}+14$$
$$=10(a-1)^{2}+4$$
よって、\(a=1\) のとき、最小値4となります。

正解だ!つまり、新しい5個の点に最もフィットする、原点を通る直線の傾きは1だということが分かったのだ。

あとは、この直線 \(y=x\) をもとの位置に平行移動すればいいのですね!
\(x\) 軸方向に3、\(y\) 軸方向に6だけ平行移動するので、
$$y-6=x-3$$
$$y=x+3$$
が求める直線になります!

うむ、正解だ!
実は、最初の図に書いた直線 \(l\) が \(y=x+3\) となっているのだ。見た目的にも最もフィットしているように見えないかな?

はい、確かに!

今回は、平行移動と微分を用いて、与えられた点に最もフィットする直線を求める方法を学んだ。この方法を数学の世界では『最小二乗法』というのだ。最小二乗法を利用して、データを分析することを、今回の題名にもなっている『単回帰分析』というのだ。さて、これで数学的な理解はできたので、次回はいよいよ単回帰分析のプログラムを書いてみよう!今回の数学的な手続きをプログラムに翻訳すればいい訳だ。次回に向けて今日の内容をしっかり理解しておいてほしい。では、今日はお疲れさん。

はい、ありがとうございました!




コメント