第25回『ニュートン法』のプログラム

はじめに
ニュートン法
オリジナルのニュートン法のプログラム

はじめに

マサト先生

やあ、こんにちは。今日は $\sqrt{2}$ や $\sqrt{3}$ などの平方根の近似値を求めるプログラムを作ってみよう。

ヒロト

はい、よろしくお願いします。

マサト先生

平方根の近似値を求める数学的な方法はいくつかあるが、

今回は『ニュートン法』という方法を利用しよう。

ヒロト

ニュートンというと、あの万有引力で有名な科学者のニュートンですか？

マサト先生

その通り。ニュートンは『世界三大数学者』の一人であり、数学の世界にも多大な功績を残したのだ。まず、ニュートン法がどういうものかを説明しよう。

ニュートン法

マサト先生

ニュートン法を用いて $\sqrt{2}$ の近似値を求めてみよう！

関数 $y=x^{2}-2$ のグラフは下のようになる。

$y=0$ のとき $x^{2}-2=0$ を解いて $x=\pm \sqrt{2}$ となるから、このグラフと $x$ 軸との交点の座標は $(\pm \sqrt{2}\ ,\ 0)$ となる。ここまでいいかな？

ヒロト

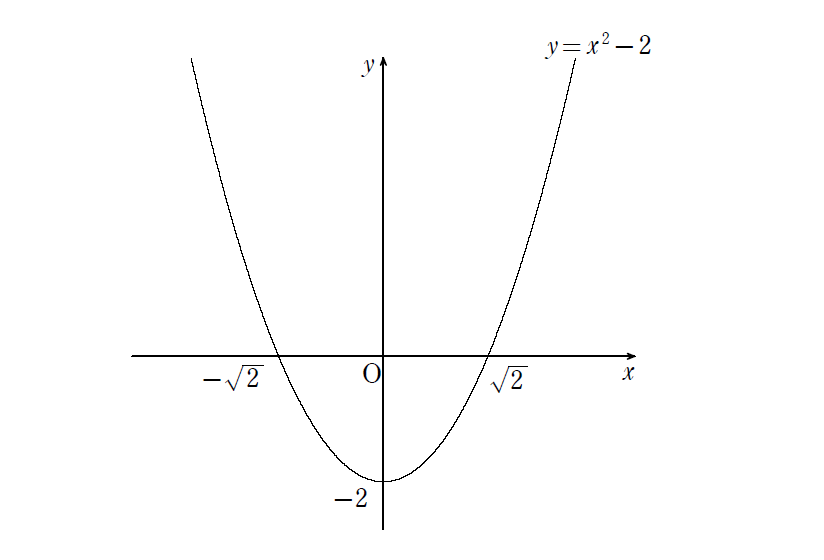
はい、全く問題なしです！

マサト先生

ここで、$f(1)=-1\ (<0)\ ,\ f(2)=2\ (>0)$ だから、グラフから $\sqrt{2}$ は $1と2$ の間に存在することが分かる。

ヒロト

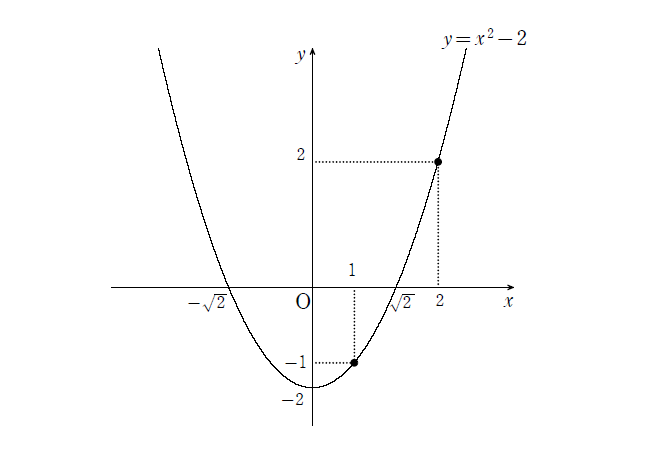
グラフから確かにそういえますね。

マサト先生

さて、今回の例の場合、$\sqrt{2}$ より大きい整数で一番小さいものは2であるが、『この $x=2$ における $y=x^{2}-2$ の接線』を求めてみよう。

必要であれば、微分積分編～第2回～を参照してほしい。

ヒロト

はい。まず、$f(x)=x^{2}-2$ とおいて微分すると、$f^{\prime}(x)=2x$ なので、$x=2$ における接線の傾きは $f^{\prime}(2)=4$ となります。また、接点は $(2\ ,\ 2)$ なので、求める接線は

$$y=4(x-2)+2\Longleftrightarrow y=4x-6$$

となります。

マサト先生

うむ、その通りだ。図に書くと下図のようになる。ここで注目してほしいのが、$y=4x-6$ と $x$ 軸との交点が $\sqrt{2}$ に近づいたということだ！その $x$ 座標を求めると、$4x-6=0$ を解いて、$x=\frac{3}{2}\ (=1.5)$ である。

ヒロト

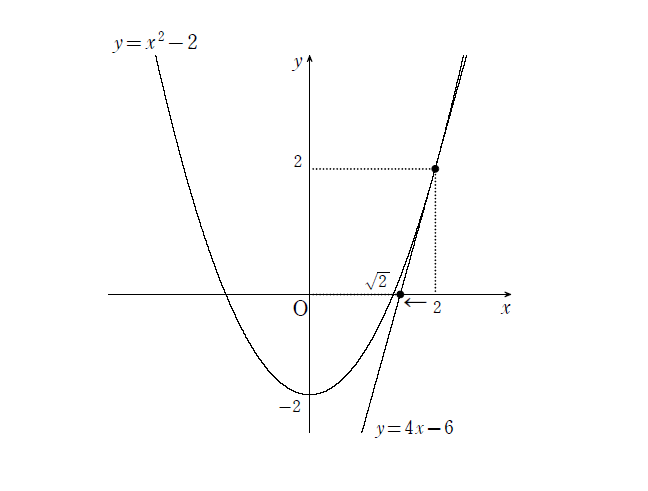
$\sqrt{2}$ の真の値である $1.414\cdots$ に確かに近づきましたね！

マサト先生

更に $x=\frac{3}{2}$ において、上と同じことをするとどうなるかな？つまり、$x=\frac{3}{2}$ における $f(x)=x^{2}-2$ の接線を求め、その接線と $x$ 軸との交点の $x$ 座標を求めるということだ。

ヒロト

はい、計算をして確かめてみますね。

$x=\frac{3}{2}$ における接線の傾きは $f^{\prime}(\frac{3}{2})=3$ となります。また、接点は $(\frac{3}{2}\ ,\ \frac{1}{4})$ なので、求める接線は

$$y=3(x-\frac{3}{2})+\frac{1}{4}\Longleftrightarrow y=3x-\frac{17}{4}$$

となります。よって、$x$ 軸との交点の座標は、$3x-\frac{17}{4}=0$ を解いて $x=\frac{17}{12}=1.415$ となります。おお！これはかなり $\sqrt{2}$ に近づきましたね！

マサト先生

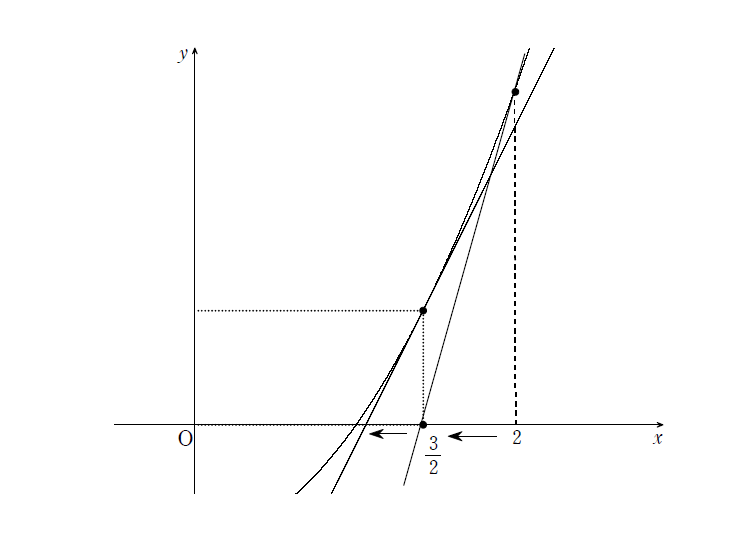
うむ、そうだろう？

このように次々に接線と $x$ 軸との交点の $x$ 座標を計算し、近似値を求める方法を『ニュートン法』というのだ。

ヒロト

たったの2回目でかなり良い近似値 $1.415$ が得られたのは驚きですね！

マサト先生

うむ、ニュートン法はいくつかある近似値を求める計算の中でトップクラスに優れた方法なのだ。さて、数学的な説明はここまでにしよう。これからヒロトにはニュートン法を実行してくれるプログラムを書いてもらおう！

ヒロト

いよいよ来ましたね！

マサト先生

まず、キーボードから好きな整数 $n$ を入力できるようにし、$n$ の正の平方根の近似値をニュートン法を10回繰り返して求めるようにしてほしいのだ。

ヒロト

はい、頑張ります！

今回は『file56』に書いていきます。

オリジナルのニュートン法のプログラム

約10分後

ヒロト

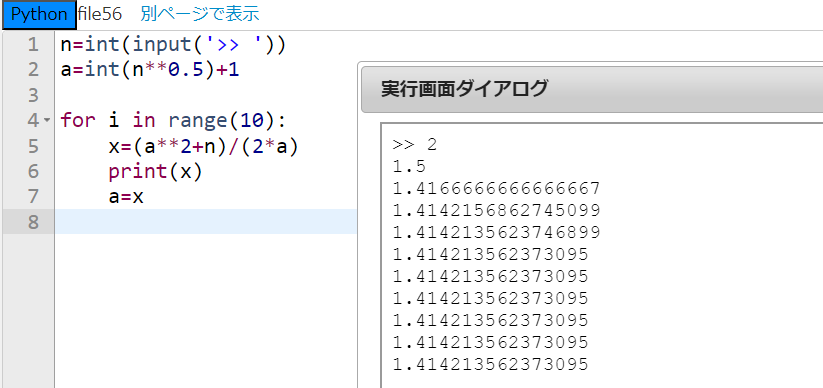
できました！思ったより短めに書けたことが意外でした。

まず、1行目でキーボードから好きな正の整数を入力するようにし、2行目は $\sqrt{n}$ より大きい最初の整数を変数 $a$ に代入しています。4行目からがニュートン法のメインとなるプログラムです。for文の回数は指定通り10回にし、5行目は $a$ における $y=x^{2}-n$ の接線と $x$ 軸との交点の $x$ 座標を計算して変数 $x$ に代入しています。6行目はその $x$ を表示し、7行目で変数 $a$ の値を $x$ の値で上書きしています。その上書きされた $a$ の値に対して同様の処理がfor文によって繰り返されるのです。