
やあ、こんにちは。今日は『最小公倍数プログラム』を作成してみよう。

はい、よろしくお願いします。

さて、早速だが手計算で42と60の最小公倍数を求めてほしい。

はい。
\(42=2\cdot3\cdot7\)
\(60=2\cdot2\cdot3\cdot5\)
なので、最小公倍数は
\(2\cdot2\cdot3\cdot5\cdot7=420\) となります。

うむ、正解だ。ヒロトの求め方は素因数分解を利用する基本に忠実な方法だな。ところで、以前『素因数分解プログラム』を作ったのを覚えているかな?確か、第21回だったと思う。そこで作ったプログラムをうまく利用すれば、今回の『最大公倍数プログラム』も作ることができそうだな。

ああ、確かに作った覚えがあります!

では、ヒントなどは不要だろう。第21回のプログラムをコピペしてから考えていいぞ。では、『最小公倍数プログラム』作成してみてくれ!

はい、素因数分解プログラムは『file51』につくっていました。それを『file53』にコピペして書いていきたいと思います。
・・・・・
・・・・・
・・・・・
約1時間後

できました!想像以上に過去一難しくかなり時間がかかってしまいました!とりあえず、下のプログラムを見て下さい。長くなったので、2枚の画像で表示しています。
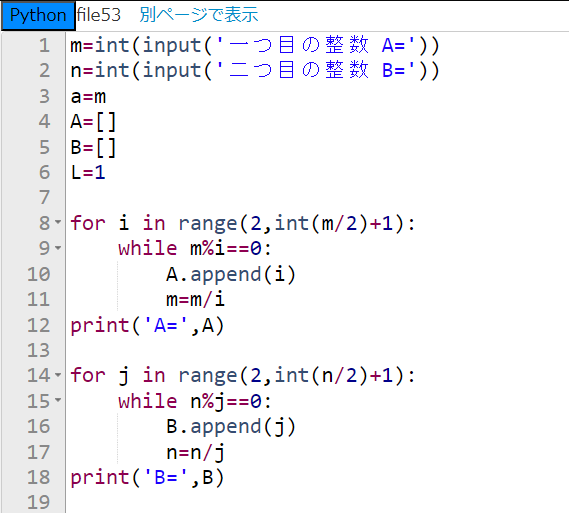

上の画像は1行目から19行目までのプログラムです。まずこれについて説明します。1・2行目ではキーボードから好きな二つの正の整数を入力します。大小関係は気にしなくて大丈夫です。3行目は変数aにmを代入しています。これは2枚目のプログラムで必要になるからです。詳しくは追って説明します。4・5行目は空のリストAとBを用意しています。そして、6行目は変数Lに1を代入しています。これは、最後に最小公倍数を計算するときに使います。さて、8行目から12行目と、14行目から18行目は、file51の素因数分解プログラムをコピペして修正したものです。ここでは入力したmとnが素因数分解され、それぞれリストAとリストBに代入されます。

ふむふむ、なるほど。ここまでで、入力した二つの正の整数mとnが素因数分解され、それぞれリストAとBの代入される訳だな。よし、いいぞ!さあ、難しいのはここからだね?

はい!ここからは書いては試してを繰返してようやくたどり着きました。では、次に続きの20行目から28行目までのプログラムについて説明します。20行目ではfor文を使ってリストBの要素でaを順に割っていきます。ここで、改めて最初に入力した整数mが必要になるのです。1行目のmは上のプログラムで上書きされてしまっているので使えないので、予め最初のmを代入した変数aを用意したのです。もし、aがBの要素で割り切れた場合は、aを上書きし、割り切れない場合はリストAにそのBの要素を追加します。これをBの要素全部に対して繰り返し、できたリストAを25行目で表示しています。26行目から28行目は追加されたリストAの要素を全てかけ合わせて変数Lに代入します。最初にL=1としておいたのはこのためです。
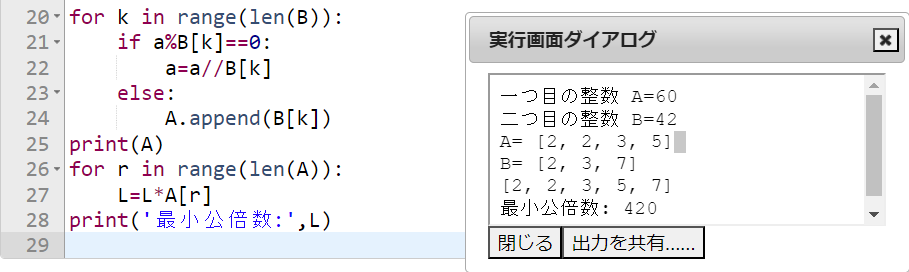

素晴らしい!上の9行のプログラムの中に必要な情報が無駄なくすべて入っている!自力でここまで出来るようになったとは本当に驚くばかりだ!

ありがとうございます!でも、何度も試行錯誤しました。
いったい何度書き直したことか・・・。

それでいいのだよ。自分で考えて書くことに意味があるのだから。
さて、『最小公倍数プログラム』は上のヒロトのものでもちろんOKなのだが、ある数学的な公式を使うともっとすっきり書けるぞ!最後にそれを紹介して終わりにしよう。

数学的な公式ですか!?

うむ。上の例を使って見せよう。42と60の最小公倍数は、420だったな。では最大公約数は何だ?

はい、最大公約数は6です!

そうだな。このとき次の等式が成り立つ。
$$42\times60=420\times6$$

\(42\times60=2520\)、\(420\times6=2520\) で確かに成り立ってますね!

ああ、公式風に書くと、
$$m \times n=G(m , n)\times L(m , n)$$
だ。

ということは、最小公倍数を求めるためには、
$$L(m , n)=\frac{m \times n}{G(m , n)}$$
を計算すればいいので、前回の最大公約数のプログラムを利用すれば一瞬で終わったということですね!

ああ、これを最初に伝えては練習にならないからあえて黙っていたのだ。もちろんヒロトが自分で気づいて使う分には全く問題なかったのだがな。でも予想以上に頑張ってくれて、本当にいい勉強になったと思うぞ。

はい、オリジナルのプログラムを書けた達成感を味わえました!
上の公式を用いた『最小公倍数プログラム』を書いてみていいですか?

もちろんだ。きっとすぐできるだろう。前回のfile52をコピペして利用するといい。

はい、新しく『file54』に書きます。
3分後

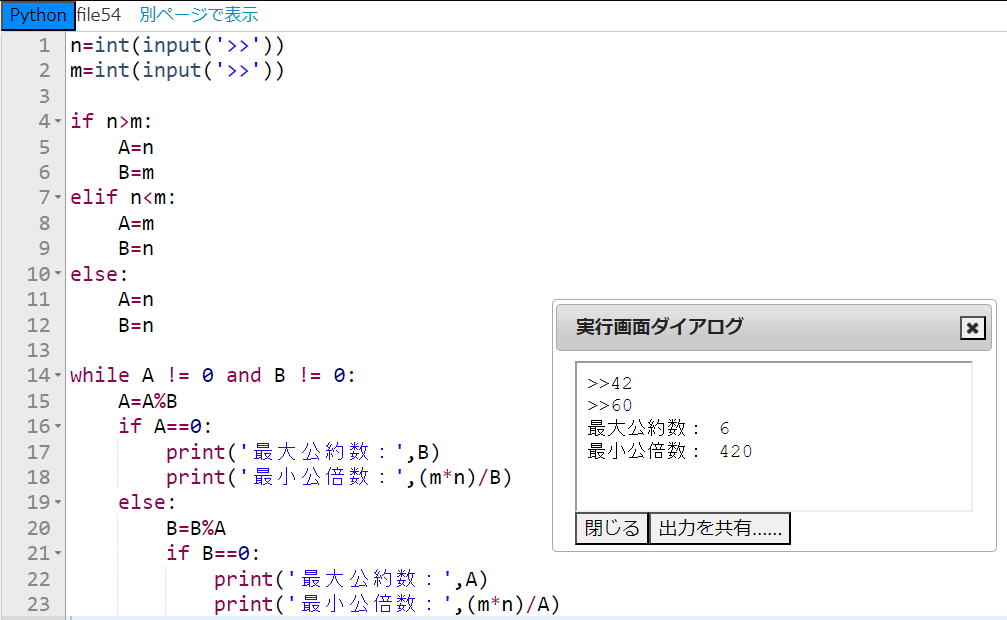
出来ました!
file52の最大公約数のプログラムをコピペして、18行目と23行目に公式を使って最小公倍数を表示するようにしました。あっという間にできました。数学の公式はプログラムを簡単にする強力なツールにもなりますね!

そういうことだ!今回はかなり大変だったと思うがよく頑張ったぞ!
疲れただろう?では今日はここまでにしよう、お疲れさん。

はい、ありがとうございました!

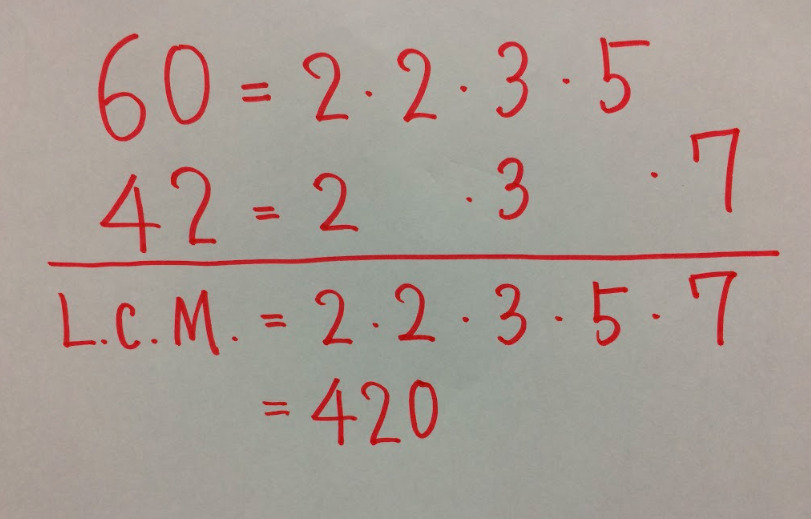

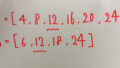
コメント