はじめに
この記事では1階微分方程式の解法の基礎を学ぶことができる。2次方程式をはじめ、これまで習ってきた方程式と名の付くものと比較すると、比較にならないほど覚えるべきことは多くあるが、しっかり順序だてて学ぶことによって無理なく習得可能である。それは、実際に手を動かして実践してきた経験があるので自信をもって言うことができるのだ。
『1階微分方程式 完全攻略』はいくつかの記事に分けて発信していこうと思う。一つ一つレンガを積んでいくように議論を進めていくので、『第一回』から順に学んでいくことをお勧めする。
1階微分方程式を初めて学ぶ人にとって少しでも役に立つことを願う。
1階線形微分方程式とは
初めに、『1階線形微分方程式』について説明していこう。
※第1回~第5回までが1階線形微分方程式の話となっている。
1階線形微分方程式とは、次の形をした微分方程式である。
$$\large y’+ a(x)y=b(x)…①$$
ここで、\(a(x) , b(x)\) は \(x\) の関数を表す。
といきなり言われてもピンとこないだろう。そんなときは具体例を見てもらうのが一番だ。例えば、次のようなものたちだ。
\(y’-2xy=x\) , \(y’+ y=\frac{1}{1+x^{2}}\) , \(y’+ \frac{1}{x} y=e^{x}\) ・・・
今後、これらを解いていくうえで大切なのは与えられた方程式を見て、\(a(x) , b(x)\) に対応する関数は何かということを見極めることだ。そうすることで、すぐに方針が立ち、どのような道具を使うのかということがすばやく分かるようになるのだ。このことは解くうえでとても大事なことなので忘れずにいてほしい。
\(a(x) , b(x)\) に対応する関数は何かということを見極める
例えば、上の具体例について、
\(y’-2xy=x\) については、\(a(x)=-2x , b(x)=x \)、
\(y’+ y=\frac{1}{1+x^{2}}\) については、\(a(x)=1 , b(x)=\frac{1}{1+x^{2}}\)、
\(y’+ \frac{1}{x} y=e^{x}\) については、\(a(x)=\frac{1}{x} , b(x)=e^{x} \) となる。
\(y’+ a(x)y=0\) の解法
さて、これから実際に解き方を説明していこう。まず、問題を簡単化して、\(y’+ a(x)y=0\) の形をした1階線形微分方程式の解法をマスターしよう。これは、右辺が、\(b(x)\equiv0\)となっている方程式だ。このように問題を簡単化して議論を進めるやり方は数学でよくやる方法なのだ。
一般的な考察をする前に、いくつかの準備をしよう!
\(y’+ a(x)y=0\) を解く上での準備
最終目標
最終的な目標は、$$\frac{d}{dx}(yの式)=f(x)$$の形にもっていくことだ。
この形に変形することができたのなら、後は両辺を \(x\) で積分して、
$$(yの式)=\int f(x) dx +C (Cは定数)$$ とできる。あとの計算は問題によってケース by ケースだ。とりあえず、最終目標は \(\frac{d}{dx}(yの式)=f(x)\) の形にするということを頭に入れておいてほしい。
最終目標は \(\frac{d}{dx}(yの式)=f(x)\) に直すこと
重要公式
そして、事前に知っておきたい重要公式がある。高校数学の数Ⅲで習った微分公式:
$$\frac{d}{dx}log|f(x)|=\frac{f'(x)}{f(x)}$$についてだ。この公式についての詳細は、まず、\(\frac{d}{dx}logx=\frac{1}{x}\) であるから、合成関数の微分法により、
\(f(x)\ge0\) のとき、\(\frac{d}{dx}log|f(x)|=\frac{d}{dx}logf(x)=\frac{f'(x)}{f(x)}\) ,
\(f(x)<0\) のとき、\(\frac{d}{dx}log|f(x)|=\frac{d}{dx}log(-f(x))=\frac{-f'(x)}{-f(x)}=\frac{f'(x)}{f(x)}\)
したがって、\(\frac{d}{dx}log|f(x)|=\frac{f'(x)}{f(x)}\) となる。
\(\frac{d}{dx}log|f(x)|=\frac{f'(x)}{f(x)}\)

\(y’+ a(x)y=0\) の具体例の解法
では、さっそく簡単な具体例から見ていこう。
例1)\(\large y’+2y=0\) を解きなさい。
\(y’+2y=0\) について \(y’=-2y\) としてから両辺を \(x\) で積分して
\(y=\int (-2y) dx\) とするのはもちろんダメだ。というのは、右辺に求めるべき関数 \(y\) が入っているので解いたことにはならないのだ。
正しくは次のようにやろう。
まず、両辺を \(y\) で割って、\(\frac{y’}{y}+2=0\) ,
ここで、上で示した公式を使うと、 \(\frac{y’}{y}=\frac{d}{dx}log|y|\) となるので、
\(\frac{d}{dx}log|y|=-2\) (←最終目標達成!), よって、両辺 \(x\) で積分して、
\(\log|y|=-2x+C_1\) (\(C_1\)は定数)よって、\(e\) の肩にのせて、\(|y|=e^{C_1}e^{-2x}\) (\(C\)は定数),
\(e^{C_1}\) は定数なので、改めて C とおくと、
\(y=Ce^{-2x}\) (\(C\)は定数) が答えとなる。
さて、いかがだっただろうか。事前に伝えた『重要公式』は『最終目標』を達成するための道具だったことが分かると思う。解答で2か所、青でアンダーラインを引いた部分がある。ここについての詳細を説明したいと思う。この説明は最初だけなので、しっかり理解してほしい。
一行目のアンダーラインについて
両辺を \(y\) で割って、\(\frac{y’}{y}+2=0\) 、とした。ここで、鋭い人は分母が0の時は割れないのでは?と思ったはずだ。まさにその通り!ただ、厳密にいえば、\(y\) は \(x\) の関数であり、かつ連続関数という前提を設けているのだ。なので、\(y\equiv0\) でないならば、\(y\) が恒等的に0ではない区間が存在する。その区間において考えているということだ。
後に触れるが、関数 \(y\) が恒等的に0ではない区間において、1階線形微分方程式の解は一意的に決定されるという定理があるので、ある区間に置いて解けば十分である。そういったことをくどくど書くことはせずに、解答のように単に両辺を \(y\) で割って・・・という書き方をしたという訳だ。
六行目のアンダーラインについて
一行上の \(|y|=Ce^{-2x}\) (\(C\)は定数) から、\(y\) の絶対値記号をとって、
\(y=Ce^{-2x}\) (\(C\)は定数) としたが、これも次のように考える人がいると思われる。
つまり、\(|y|=Ce^{-2x}\) (\(C\)は定数) から、\(y\) の絶対値記号をとったら、
\(y=\pm Ce^{-2x}\) (\(C\)は定数) となるのではないか?
うむ、ご尤もだ!ただし、次の理由から\(\pm \) はつけなくて良いことが分かるのだ。
今、\(y=\pm Ce^{-2x}\) を両辺に \(e^{-2x}\) をかけて変形すると、
$$ye^{2x}=\pm C $$
となる。ここで注意してほしいのは左辺は連続関数であるということだ。そして、定数 C はもともと、\(e^{C_1}\) という形をしていたので、これは0でない定数だ。
よって、もし、$$ye^{2x}=\pm C $$ が成り立つ、すなわち、連続関数が異なる二つの値:
\(C , -C\) をとるならば、それは連続関数ではなくなってしまうのである。(下図を参照)
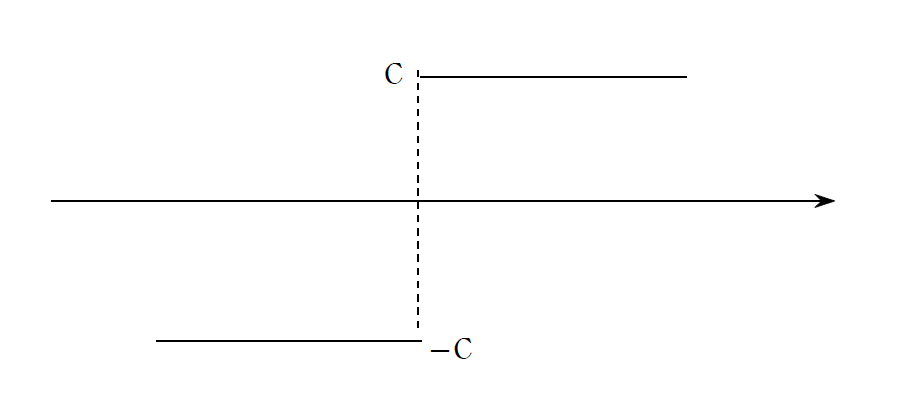
したがって、\(|y|=Ce^{-2x}\) (\(C\)は定数) から、\(y\) の絶対値記号を取るとき、
単に絶対値を外して、\(y=Ce^{-2x}\) (\(C\)は定数) として良いのだ。
細かい話だったが、こういうところをあいまいにすると、完全にすっきりしないものだ。
今後の議論においては、解答の煩雑さを避けるため、上記のことをいちいち断らないので、よろしく頼む。
今後は、\(y\)で両辺を割ることや、\(y\) の絶対値記号を取るということを当たり前にやっていく
さて、第一回の最後に、上記注意に気を付けて、次の例題を簡潔に解いてみよう!
例2)\(\large y’+(sinx)y=0\) を解きなさい。
まず、両辺を \(y\) で割って、\(\frac{y’}{y}+sinx=0\) ,
\(\frac{y’}{y}=\frac{d}{dx}log|y|\) となるので、\(\frac{d}{dx}log|y|=-sinx\) (←最終目標達成!),
よって、両辺 \(x\) で積分して、\(\log|y|=cosx+C_1\) (\(C_1\)は定数)よって、
\(|y|=e^{C_1}e^{cosx}\) 、\(e^{C_1}\) は定数なので、改めて C とおくと、
\(y=Ce^{cosx}\) (\(C\)は定数) が答えとなる。
第一回の最後に
さて、いかがだっただろうか?第一回は、細かいことも説明する必要があって長くなったが、次回からは細かい部分は多少飛ばして、サクサク進んでいこうと思う。
焦らず、毎日無理なくコツコツと進めていくことが大切だ。
では、またディープな数学の世界で会おう!



コメント