『Matplotlib.pyplot』について

やあ、こんにちは。今日は『グラフの作成』についてやっていこう。

はい、よろしくお願いします。

今回は『matplotlib.pyplot』という、あらかじめ組み込まれたプログラムを用いてグラフを描いていく。これを使うためには、プログラムの1行目に『import matplotlib.pyplot as plt』と書く必要がある。

第10回で『タートルグラフィックス』を使った時も同じことをしましたね。つまり、matplotlib.pyplot を『plt』として呼び出すということですね!

そういうことだ。pltを呼び出すことによって、様々な機能が使えるようになるぞ。はじめに『plt.scatter関数』を用いて散布図を描こう。下の画面を見てほしい。
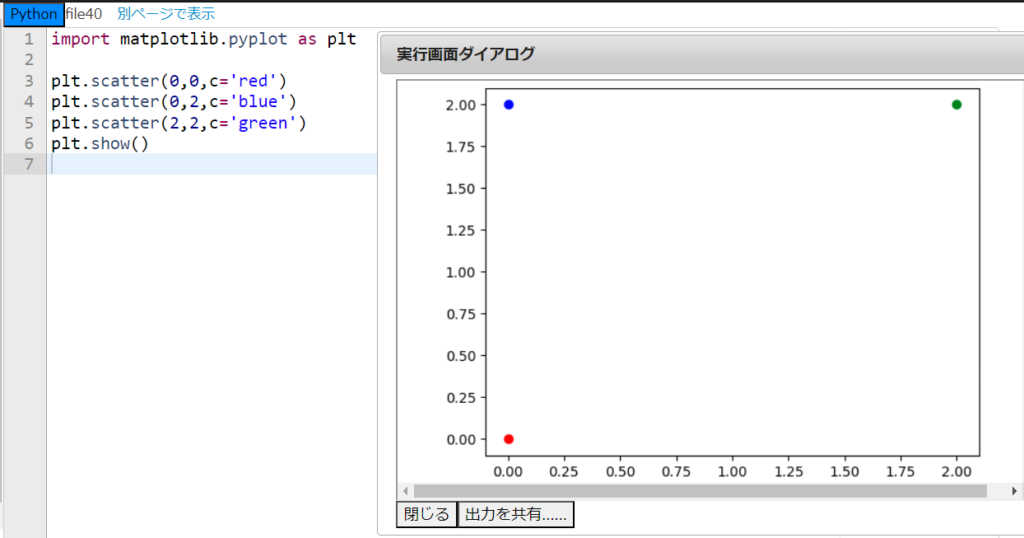

上のプログラムでは、『plt.scatter関数』を用いて点を3個表示している。
『plt.scatter( x , y , c=’ 色 ‘ )』という」形をしているが、xがx座標、yがy座標、c=’色’で点の色を指定できると言うわけだ。そして、6行目の plt.show() で画面に表示することになる。

なるほど、cは『color』の頭文字だったのですね!

うむ、それから今回のプログラムを実行するときは全て『サーバで実行』することに注意してほしい。どういうことか覚えているかな?

はい、ビットアロー画面上部にある『実行』をクリックすると、『サーバで実行』が選択できるのでした。

そういうことだ。では次に画面に直線を描いてみよう。

直線や曲線を描く

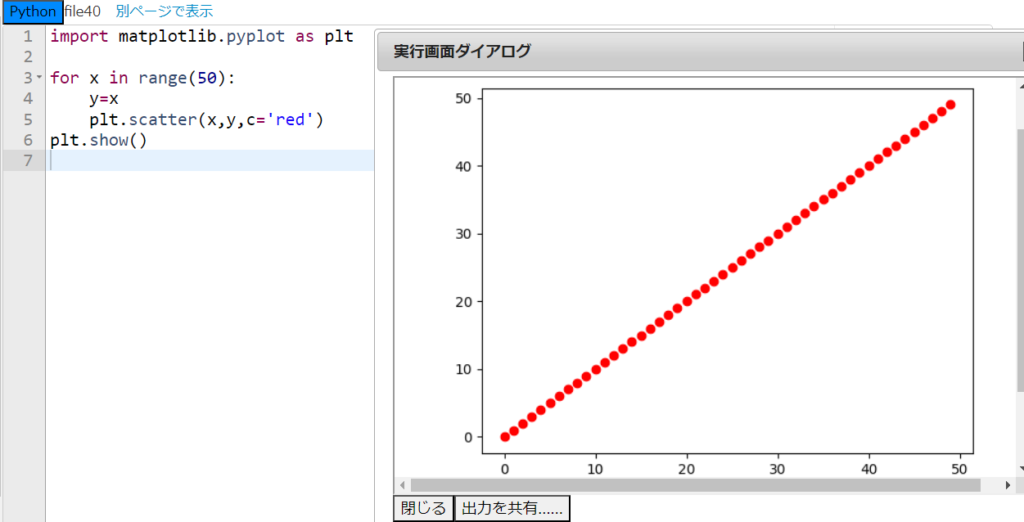
for文を使うと、点を少しずつ変化させて直線や曲線を描くことができる。次のプログラムを見てほしい。


上のプログラムでは、for文によって変数xに0から49までの値を代入しながら、y=x を満たす点の座標をplt.scatter関数に代入している。このプログラムを実行するとどうなるか考えてほしい。

はい、これは『y=x』という直線が描かれると思います。厳密には50個の点が描かれるということですが。実際に実行して確認してみます。今回は『file40』から始めます。

うむ、良さそうだな。では、上のプログラムを利用して『y=-2x+5』の直線を描くプログラムを書いてみて欲しい。ただし、直線の色は青とする。

はい、これはこことここを書き換えるだけで良さそうですね!
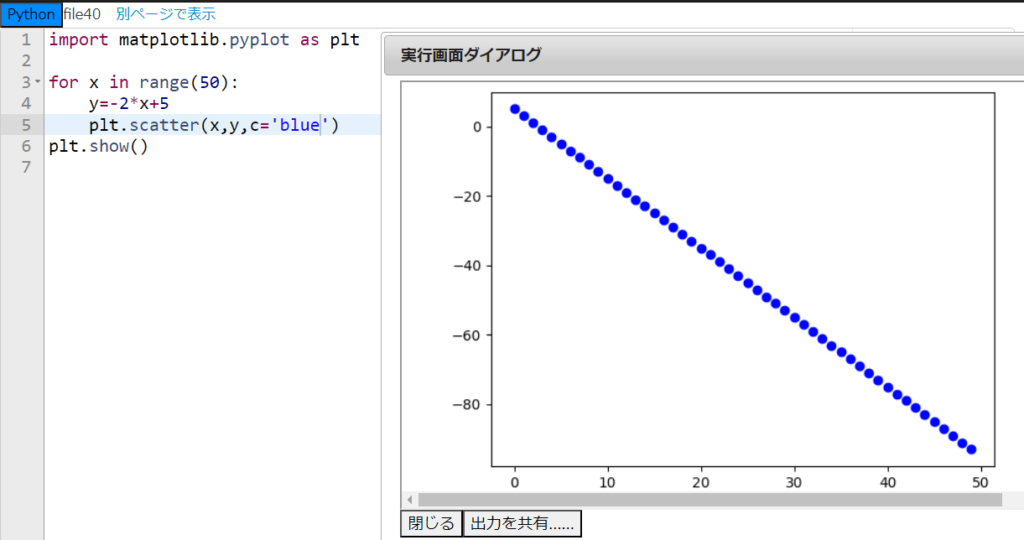

できました!4行目の直線の式と、5行目の色をblueに書き換えただけなので簡単でした!

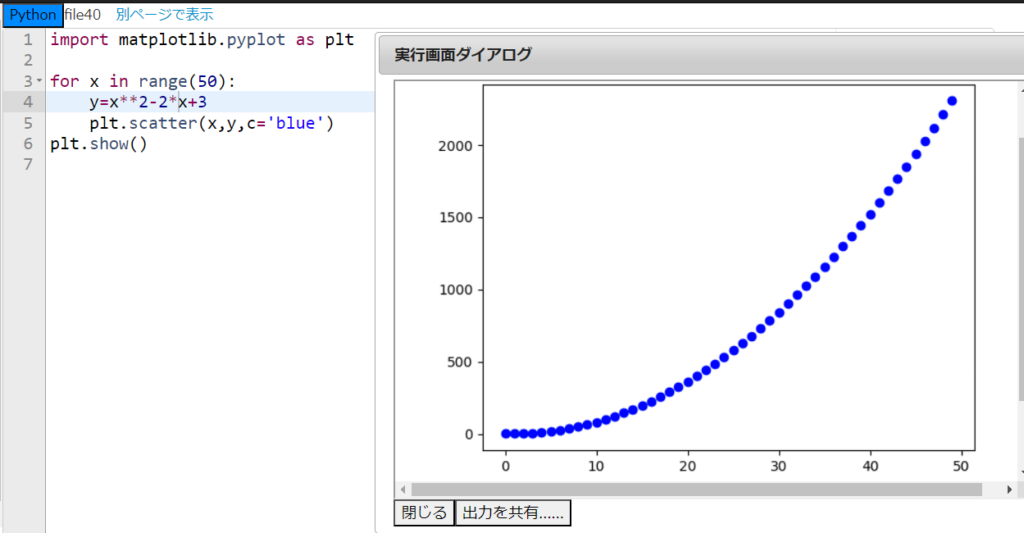
うむ、そこに気づいたのならもう大丈夫だ。そうすると、2次関数
$$y=x^{2}-2x+3$$
のグラフもすぐ描けるだろう?

はい、これも4行目を書き換えるだけで行けると思います。これも同じfile40に書きます。

三角関数のグラフ

次に、三角関数のグラフを描いてみよう。これはこれまでのように簡単にはいかないぞ。まず、『math』というプログラムを呼び出す必要がある。次の画面を見てほしい。
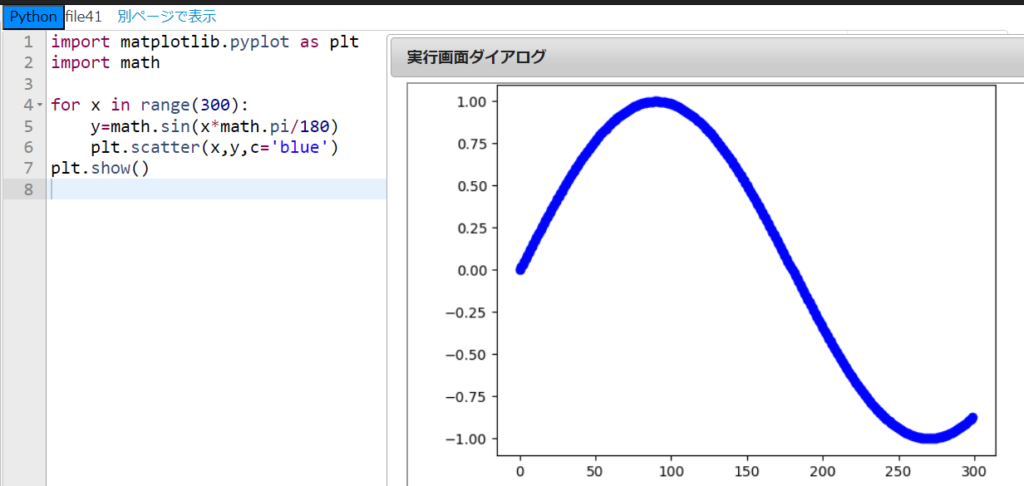

上のプログラムでは、2行目で新たに『math』を呼び出している。そして、5行目の『y=math.sin(x*math.pi / 180)』は数式で、
$$y=\sin (\frac{\pi x}{180})$$
を意味するプログラムだ。サイン関数や円周率の \(\pi\) を使うときは先頭に『math.』をつけて『math.sin(・・・)』や『math.pi』のように表すことに注意してほしい。

はい、角度としては『ラジアン』を使っているのですね!

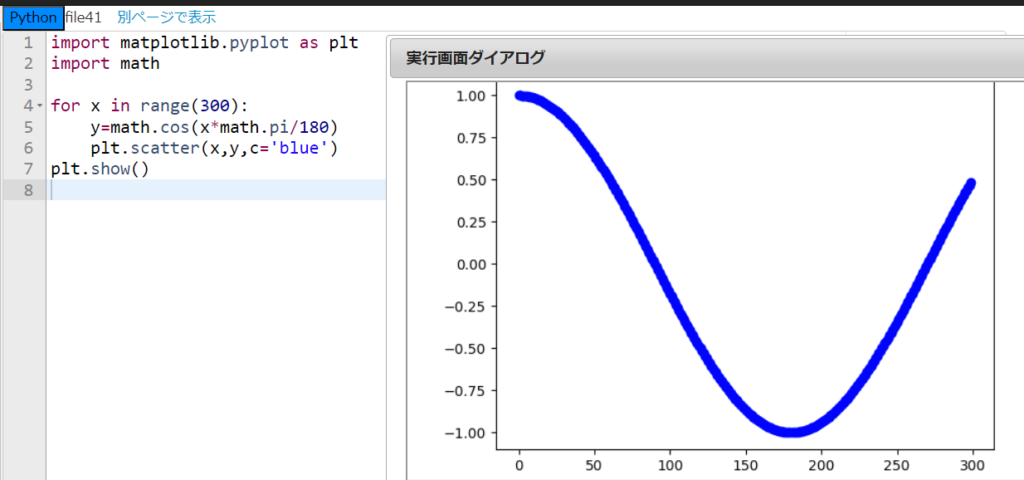
そういうことだ。上のプログラムを利用して、新しい『file41』に『y=cosx』のグラフを描いてごらん。

はい、これはここをこう書き換えるだけですね!
折れ線グラフを描く

では、最後に折れ線グラフを描いてみよう。まずは下の画面を見てほしい。
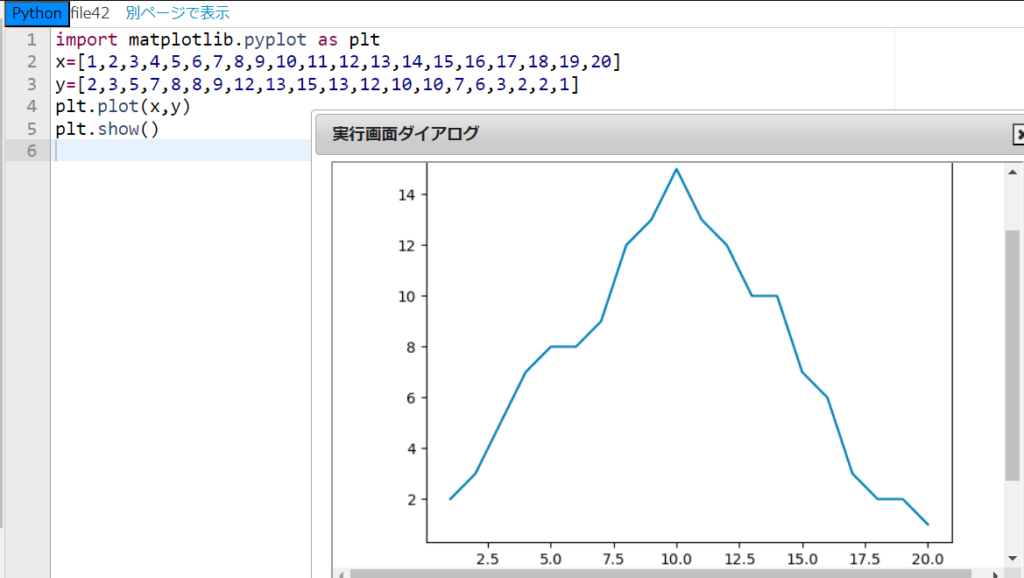

上のプログラムでは、与えられたデータのリスト x と y をもとに折れ線グラフを描いている。このように点のデータは、リストとして渡す必要があり、5行目の『plt.plot関数』で折れ線を表示できるのだ。

おーこれは便利ですね!x と y のデータは何でもいい訳ですね!

うむ、y座標のデータを次のように、y1とy2の複数用意することによって、複数の折れ線グラフを描くことができるぞ!実際に書いて実行してみるといいだろう。
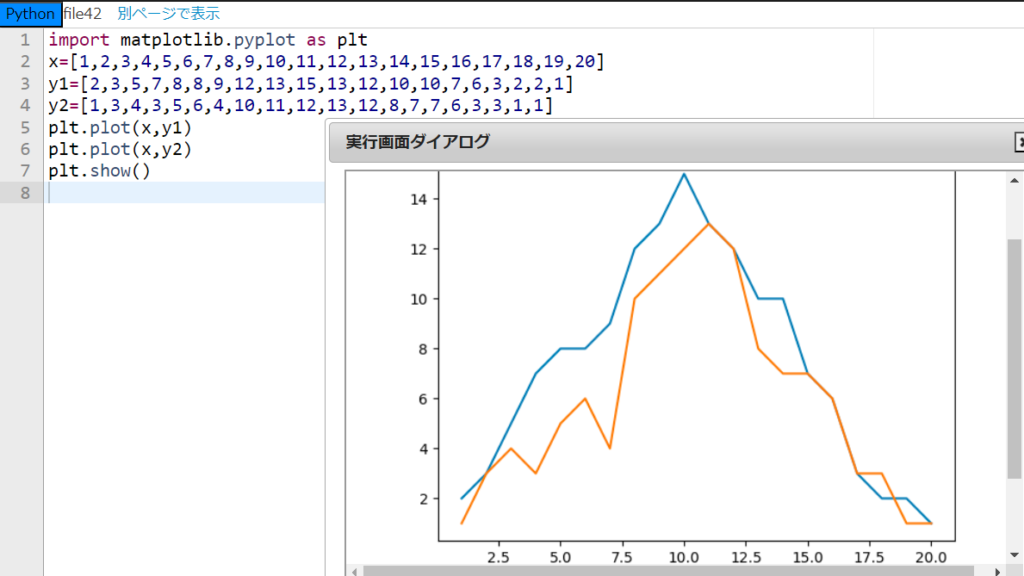

なるほど、y のデータリストだけを増やしていけば同じ画面上に表示できるのですね!

ランダム関数の視覚化

うむ、では最後に一つ問題を出すぞ!
x=[1 , 2 ,・・・, 100] とする。ランダムに1から100までの100個の整数を入れたリスト y を作り、折れ線グラフを描いてみよう。

まず、x のリストを作るのが大変ですね。これは、for文とappend関数を使ってリストx に1から100まで追加していけば良さそうですね!そして確か『random.randint(1,100)』で1から100までの整数がランダムに1つ作られます。これを、やはりfor文とappend関数を使ってリストy に追加していくという方針でやってみよう!新しくfile43に書きます。
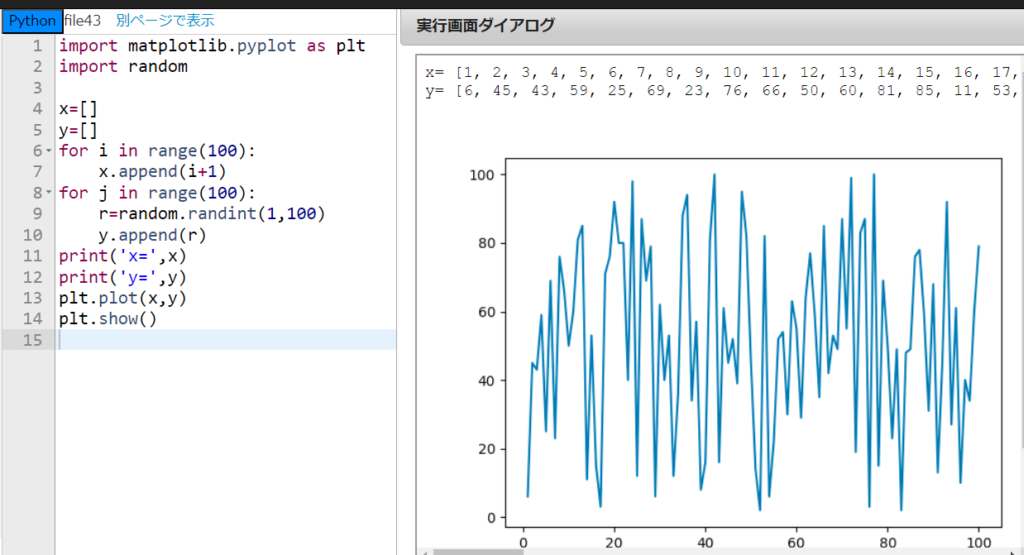

できました!
for文、random関数、append関数の3つを用いて書きました!

素晴らしい!
ランダム性を実際に目で見ることができたわけだ。どうだ?これがランダムというものだ。

はい、全く規則性がないですね!

さて、今日はここまでにしよう。次回は『関数を定義する』ことについて学ぼう。では今日もお疲れさん。

はい、ありがとうございました。




コメント