はじめに

やあ、こんにちは。今日は『関数の定義』についてやっていこう。

はい、よろしくお願いします。
早速ですが、関数を定義するというのはどういうことですか?

これまで用いてきたprint関数などの関数を、自分なりに定義して、好きな時に呼び出すことができるのだ。関数を定義するときは『def』を用いて以下の形で定義する。
def 関数名(引数):
処理

と言われてもピンとこないだろう?まずは、下の具体例を見てほしい。
引数を使わない場合


f() の () の中の変数を『引数』というが、上のプログラムは引数を使わない場合のものだ。
f() という関数の処理を、print関数を用いて定義していると理解してほしい。この新しく定義した関数 f() を使いたいときはそのまま f() と書いて実行すればいい。下の画像を見てほしい。
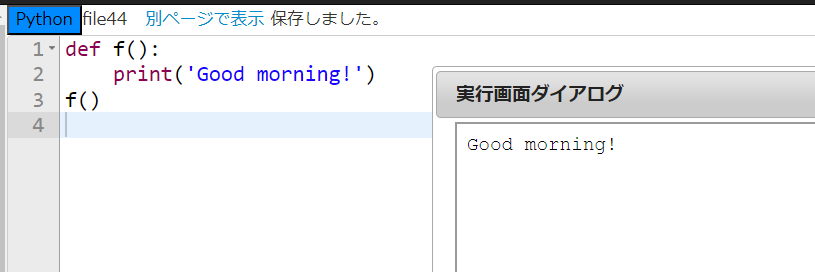

定義した通り、『Good morning!』が表示されましたね!一度定義してしまえば、f()とだけ入力すればいいので便利ですね!

ああ、よく使うあいさつなどの定型文を定義すれば便利だな。
次に引数を使う場合を見てみよう。次の画像を見てほしい。

引数を使う場合
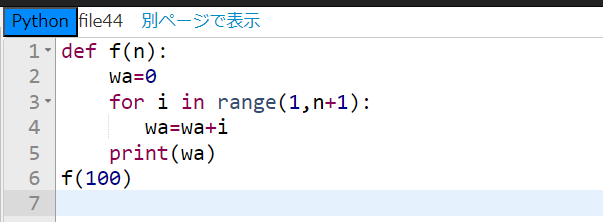

上のプログラムは、f() のカッコの中に引数 n が入っている場合のものだ。そして、この関数を定義する処理の部分を見てみると、まず2行目で wa という変数に0が代入されていて、3行目のfor文においては1からn+1未満の整数が i に代入され、wa に足されていくことになっており、5行目で wa を表示するところまでがこの関数の定義だ。6行目でこの関数をn=100として呼び出しているところだ。すると、この関数 f(n) の処理は n=100 として実行されることになるのだ。

なるほど、n の値は好きに決めていいのですね!今回のプログラムは、1から n までの和を求める関数を定義したことになっているので、f(100) は1から100までの和を教えてくれるはずです。

うむ、実際に書いて実行して確認してごらん。

はい、今回は『file44』から始めます。
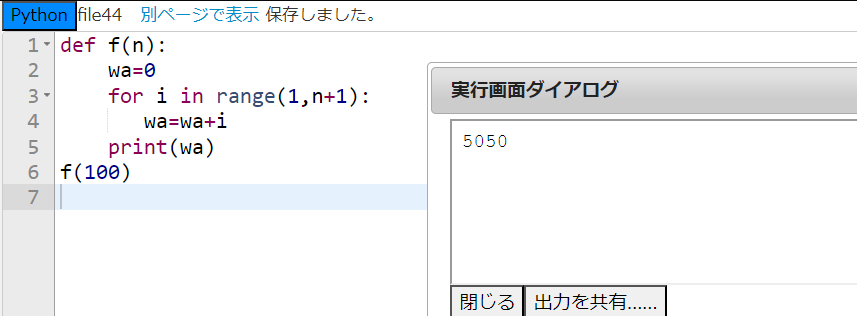

おお、しっかり1から100までの和が計算されましたね!
自分で計算器を作ったみたいですね!

うむ。では一つ問題を出すぞ。
『半径を引数として渡すと、円の面積を計算してくれる関数を定義してみよう』

はい、これは新たにfile45に書きます。
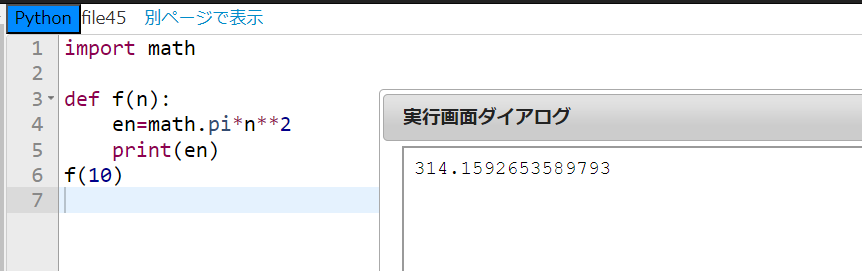

できました!『file41』のプログラムでやったように、1行目に『import math』と書いて円周率 \(\pi\) を使えるようにしました。4行目と5行目が円の面積を求める関数の定義です。4行目は en という変数に円の面積 \(\pi \times n^{2}\) を代入しています。

完璧だ!
今回は関数の定義についてやったが、これはいろいろ応用できるのでぜひプログラムを書くときは意識してほしい。

確かにとても応用が利くものだと思いました!

うむ。では今回はここまでにしよう、お疲れさん。

ありがとうございました!




コメント