はじめに

やあ、こんにちは。今日は2種類のプログラム
『貯金残高シミュレーションプログラム』、
『お釣りの計算プログラム』
についてやっていこう。

はい、よろしくお願いします。

残高シミュレーションプログラム

まずは、『貯金残高シミュレーションプログラム』についてだが、例えば10万円を金利1%の銀行に貯金した場合、10年後には貯金額がいくらになっているのかプログラムで予想してみよう。

預けたお金が何年後かにはいくらになっているのかを事前に計算で知ることができるのはうれしいですね!

うむ。プログラムを書く前に基本的なことを説明すると、貯金額に金利をかけることによって、1年後の利息が計算できる。利息というのは預けているだけでもらえるお金のことだ。今回の場合、利息は \(100000 \times 0.01=1000\ (円)\) となる。その結果、1年後の貯金額は利息の分だけ増えて、\(101000\ (円)\) となる。ここまでいいかい?

金利は 1%=0.01 として計算したのですね!
2年目の利息は、\(101000\ (円)\) に0.01をかけて求めるということでいいのですね?

察しが良いな、その通りだ!つまり、2年目の利息は、
\(101000\times 0.01 =1010\ (円)\) となり2年目の貯金額は利息の分だけ増えて、
\(101000+1010=102010\ (円)\) となるわけだ。
このように毎年『貯金額+利息』が新たな利息を計算するための貯金額になる、
という計算法を『複利計算』というのだ。

複利計算ですね、分かりました!どんどん上乗せされていくので嬉しい計算法ですね!

では、以上の情報をもとにしてプログラムを書いてみよう!
ビットアローの準備はいいかな?

はい!今回はfile26を新しく作成します。10年後の貯金額を求めるので複利計算を10回繰り返すことになりそうですね、ということはfor文の出番かな?

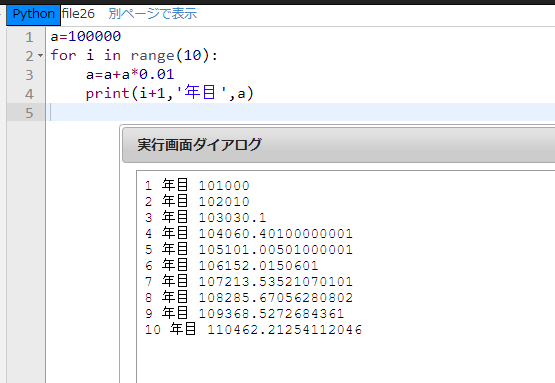

できました!
まず、変数 \(a\) に100000を代入して、2行目でfor文の回数を10回にしました。3行目では変数 \(a\) に毎年の貯金額を上書きするようにしました。4行目では毎年の貯金額をprint関数で表示するようにしました。

うむ、よくできているぞ!10年後には110462円になることが分かったわけだ。
一つだけアドバイスしよう。今回は金利1%だったが、金利というのはよく変化するものなのだ。そこで、上のプログラムにおいて新たに変数 \(b\) を用意して、それに0.01を代入し、\(b\) を用いて同じプログラムを書くのだ。

なるほど、とにかく書き直してみますね!
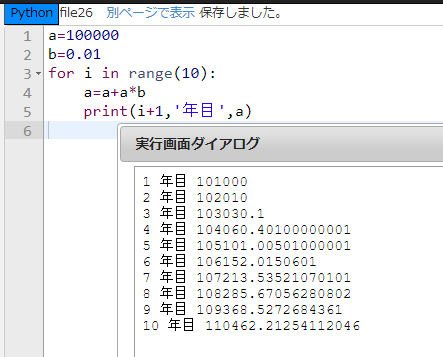

2行目に新しく金利0.01を代入した変数 \(b\) を用意しました。そして、4行名の式を \(b\) で書き換えました。

完璧だ!
このように新たに変数 \(b\) を用意することで、もしも金利が変化したとき、\(b\) に新しい金利を代入するだけでプログラムを再利用できるようになるだろう?

なるほど、書き直す箇所が1か所だけで済むということですね!これは使えるテクニックですね!

今でなくていいので、元金 \(a\) の値や、金利 \(b\) の値を色々変えて結果を確認してみよう。さらに預ける年数も10年から20年に変えたりして結果をシミュレーションしてみよう!

はい、いろいろいじって遊んでみます。

お釣りの計算プログラム

では次に『お釣りの計算プログラム』についてやっていこう。これはつまりお店にあるレジみたいなもので、購入金額に対して支払った金額から、お釣りとして渡す紙幣や硬貨の枚数を計算するプログラムのことだ。

このプログラムも購入金額と支払った金額を表す二つの変数を用意すると良いですね。

その通りだ。例えば購入金額が300円で、支払った金額が5000円だった場合、お釣りは5000-300=4700(円)になるから、千円札4枚、500円玉1枚、100円玉2枚ということになる。問題は、お釣りの紙幣の枚数と硬貨の枚数をどうやって求めるかだ。それが分かればプログラムを書けるようになるだろう。

はい、4700円の中に千円札が何枚含まれるかを求めるためには4700を1000で割ったときの『商』を求めればよいです。そして、500円玉の枚数は、残りの700を500で割ったときの『商』を求める。以下同様となります。

その通りだ!
ある数をある数で割ったときの商を計算してくれる便利な演算があったことを覚えているかな?


うむ、そうだったな。ここまで準備すればもう大丈夫だろう。では、後は自分で考えてプログラムを書いてみよう。

はい、頑張ります!

約10分後
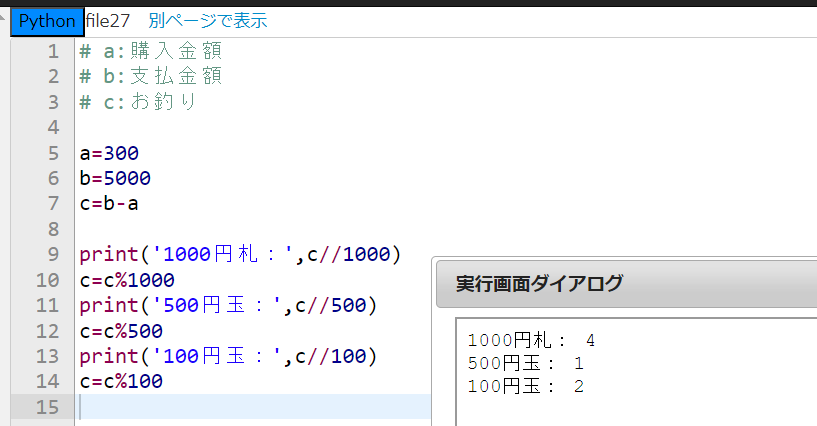

できました!お釣りが正しく計算されました。

うむ、今回の場合はそれでいいが、例えば312円の物を買ったとして1万円札しかなかった場合どうなるだろう。お釣りは、10000-312=9688(円)となって、5千円札、千円札、500円玉、100円玉、50円玉、10円玉、5円玉、1円玉の全ての枚数を計算する必要があるだろう。

確かに!ということは数字だけを変えた同様の計算をコピペで増やせばいいですね!しばしお待ちを。

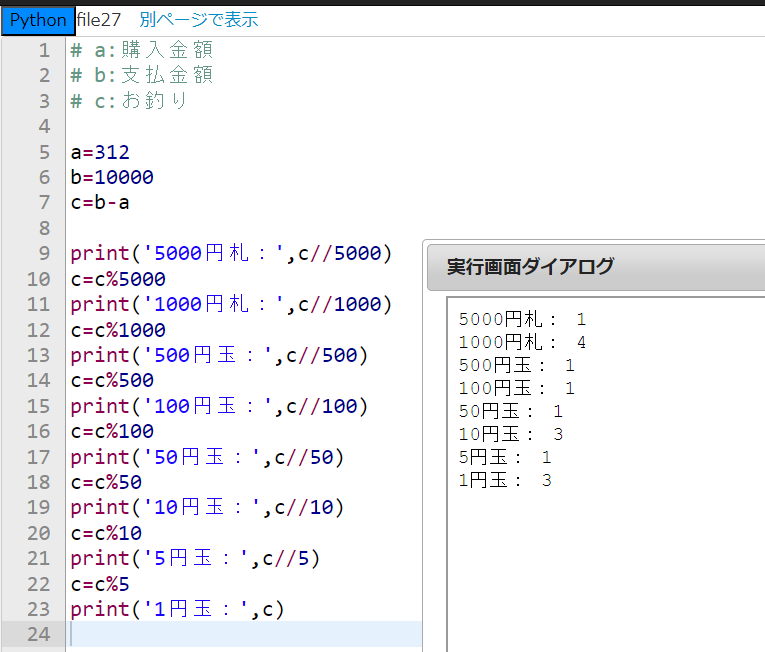

できました!これでどんな場合にも対応できると思います!

素晴らしい!
\(a\) と \(b\) の値を色々と変化させて結果を確認してみるといいだろう。

はい、いくつか試しましたが大丈夫そうです。自作のレジマシンの完成です!

これで、いつでもお店が始められるな!順調にいったことだし今回はここまでにしよう。次回は『while文』についてやろうと思う。では、お疲れさん。

はい、ありがとうございました!




コメント