はじめに

やあ、こんにちは。今日は『素数判定プログラム』を作成してみよう。

はい、よろしくお願いします。

素数判定プログラムとは、文字通り与えられた整数が素数かどうか判定してくれるプログラムのことだ。自分で好きな整数を入力して、それが素数ならば『素数』、素数でないならば『合成数』と表示するようにしたい。その前に、素数がどういうものかはもちろん知っているな?
素数の定義

はい!素数は1と自分自身のみを約数として持つ正の整数のことです。小さい方から2,3,5,7,11,13…と続きます。また、素数は無限に存在することが知られています。

うむ、大丈夫そうだな。実際にプログラムを書く前に少し準備をしよう。与えられた整数、例えばそうだな『1001』は素数かどうか調べてほしい。

1001ですか・・・素数のような気もしますがはっきりしません。こういう時は2から順に割り切れるかどうかチェックしていくのでした。2はもちろんダメで、3もダメ、5もダメ・・・ええと、7では1001=7×143となって割り切れました!よって1001は素数ではありません。つまり合成数ということになります。

うむ、その通りだ。因みに、1001=7×11×13と因数分解されるぞ。さて、プログラムで与えられた整数が素数かどうか調べるときも、基本的には上でヒロトがやったのと同じ方法を取る。つまり、2から順に割り切れるかどうかチェックするのだ。

なるほど、2から順に繰り返し割っていくので、おそらく『for文』の出番でしょうね!
使う道具

うむ、あとは割り切れるという状況をどう表現するかが問題だ。何か使えそうなものはあるかな?

うーん、例えばある整数で割ったときの余りを求めてくれる演算があったと思います。確か『%』を使うのでした。なので、2から順に割った余りを求めていき、それが0になったら終了という風にすればいいと思います。

うむ、方針が立ってきたみたいだな。では、そろそろプログラムを書いてみよう!

はい、今日は『file50』から書いていきます。
約10分後
自作プログラム

できました!
1行目で素数かどうか判定したい整数を入力します。2行目であらかじめ変数 a に『素数である』という文字列を代入しておきました。ここ、自分的にはとても工夫した点です!4~6行目のfor文で2からn-1までの整数で割った余りが0になるかどうかチェックしています。もし、余りが0になることがあれば変数 a に『合成数である』という文字列を上書きします。もし、入力した整数が素数であった場合は、上書きされずに7行目で素数であると表示されます。
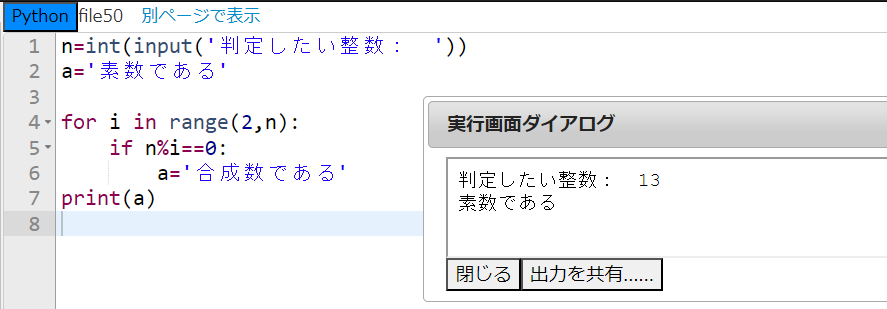

素晴らしい、とても短くまとまっていて見事なプログラムだ!2行目であらかじめ変数 a に『素数である』という文字列を代入したという工夫、簡単そうに見えてなかなか思いつかないものなので立派だぞ。

はい、ありがとうございます!
より良くするために

一つだけアドバイスをしよう!例えばかなり大きな整数が素数かどうか調べるとき、2からn-1まで割るのは効率が悪い。たとえば『1234567』という整数を上のプログラムで調べると数秒かかってしまうのだ。たいしたことないと思うだろうが、コンピュータで数秒はとてつもない作業をしていることになるのだ。

はい、今試しましたが、2、3秒かかりました。もっと大きい数になるともっと時間がかかるようになると予想されますね?

そういうことだ。そこで、作業の量を劇的に減らす方法を教えよう。結論から言うと、整数 n が素数であるかどうか調べるには、2から \(\sqrt{n}\) まで割り切れるかどうか調べれば十分なのだ。\(\sqrt{n}\) には小数が含まれることがあるため、int関数で切り捨てて整数を作り、for文の範囲を『range(2 , int(n**0.5)+1)』としてやればいいのだ。

へえ、そうなんですか!先ほどの1001はおおよそ、\(\sqrt{1001}=31.64\) なので、2から31までチェックすればいいことになります。これは劇的に作業が減りますね!999回の計算が31回になるのですから!でも、どうしてなのでしょうか?

ふふ、とても簡単な理屈なのだ。分かりやすさのため、例えば100を例にとって説明しよう。
\(\sqrt{100}=10\) であるから2から10まで100の約数があるかどうかチェックすればいい訳だが、10より大きい約数が存在するかどうかは調べる必要がないのだ。例えば、20は10より大きい100の約数であるが、これは100=20×5であるから5で割ったときに既にチェック済みなのだ。また、25も10より大きい100の約数であるがこれは100=25×4であるから4で割ったときに既に調べている。

なるほど、100未満の最大の約数である50は2で割ったときに既にチェック済みということですね!したがって、2から \(\sqrt{n}\) までの整数で割り切れなければ、\(\sqrt{n}\) より大きくn-1以下の整数でも割り切れないことが自動的に言えるわけですね。

そういうことだ!
では、このことを踏まえて上のプログラムを修正してみよう!

はい、for文の範囲を変更すればいいのでしたね。
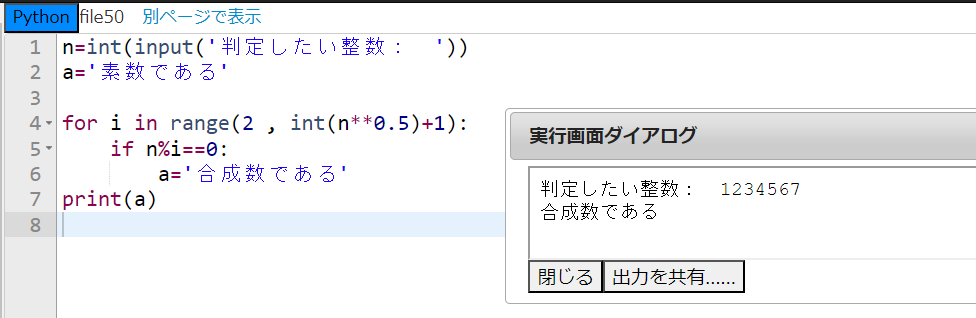

できました!4行目のfor文の範囲だけを修正しました。
さきほどの『1234567』を試してみたところ、修正前は2,3秒かかっていた作業が、修正後はほとんど一瞬で終わりました!

うむ、このようにプログラムをより良くするためには数学的な知識も必要となることは覚えておいてほしい。では今日はここまでにしよう、お疲れさん。

はい、ありがとうございました!




コメント