第二十一回　素因数分解プログラム

はい、よろしくお願いします。

はい、例えば

$$100=2^{2} \times 5^{2}$$

と素因数分解されます。

はい、頑張ります！

どうして前回と同じ２から \(\sqrt{n}\) までではなく、2から \(\frac{n}{2}\) までなのですか？

なるほど、与えられた整数 n の素因数として最大となるのは自分自身を除くと \(\frac{n}{2}\) だからですね！

はい、空のリストを用意するには『 A=[ ] 』と書くのでしたね。

ええと、確か『A.append(2)』と書くことにより、空のリストAに要素2が1個追加されます。

要するに、2で割り切れる限りリストに追加し続ければいいのですよね？

つまり、\(100 \div 2 = 50\) だから、次に \(50 \div 2 =25\) という風に、2で割り切れる限り割り続けていき、割り切れなくなったら次の数3に移るという方針はどうでしょう？

はい、『while文』はある条件を満たすときに処理を繰返してくれるものでしたね！今回は『file51』から書いていきます。では、ちょっと格闘してきます！

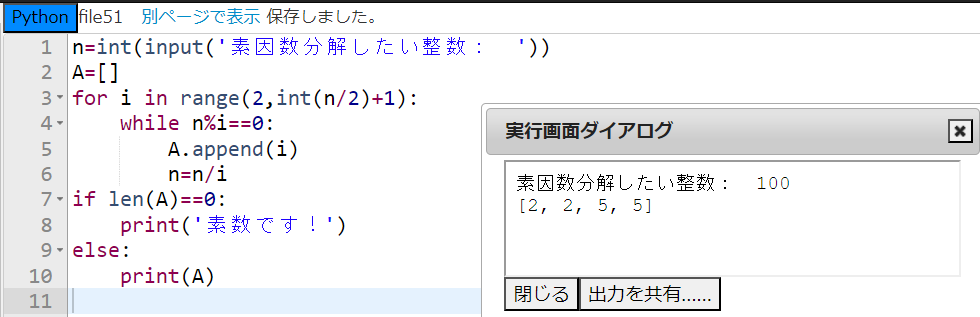
ふう、やっとできました！これからプログラムの説明をします。

1行目で素因数分解したい整数 n をキーボードから入力します。2行目で空のリストAを用意しています。3行目のfor文の範囲は、2から \(\frac{n}{2}\) の整数部分までです。for文については、まず i に2が代入されて、4行目のwhile文の条件により、n が2で割り切れるとき、5行目によってリストAに2が追加されます。6行目では、n を 商 \(\frac{n}{2}\) で上書きしています。while文は次に、この上書きされた整数に対して同じく2で割り切れるかチェックします。2で割り切れなくなったら i=2 の場合のwhile文のループは終了し、こんどはfor文のループにより i に3が代入されて同様の処置が繰り返されるわけです。最終的に7行目でリストAが空のまま、つまり2から \(\frac{n}{2}\) までに素因数がなかった場合、自分自身が素数となるので『素数です！』と表示し、2から \(\frac{n}{2}\) までに素因数があったら、 n の素因数すべてが追加されたリストAをプリント関数で表示しています。上の例では\(100=2^{2} \times 5^{2}\) より、A=[2,2,5,5] と表示されています。

はい、ありがとうございます！

はい、お任せあれ！

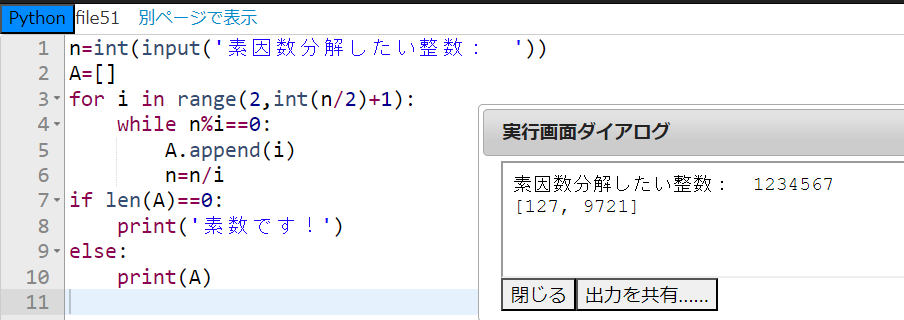
できました！結果は

$$1234567=127 \times 9721$$

でした！

はい！とてもうれしいです！

はい、ありがとうございました！