はじめに

やあ、こんにちは。今回は実際に大学入試に出された最大値・最小値を求める問題をやっていこう。

はい、よろしくお願いします!


前回の最後にも伝えたが、
$$『(導関数)=0\ を解くことで最大値・最小値を求めることができる』$$
ということを念頭に置いて解いてほしい。

微分は最大値・最小値問題を『方程式を解く問題』に帰着してくれるのでした!

うむ、大丈夫そうだな。では、さっそく問題を見ていこう!
問題
問題1
次の関数の最大値を求めよ。
$$f(x)=\frac{\log x}{\sqrt{x}}$$
問題2
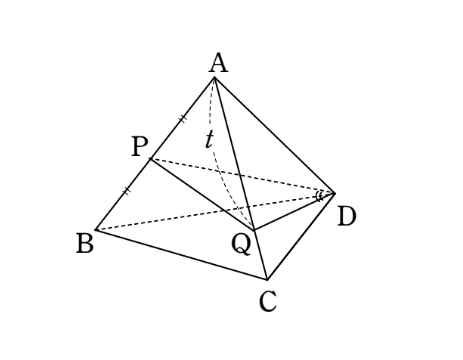
1辺の長さが1の正四面体 \(ABCD\) において、\(P\) を辺 \(AB\) の中点とし、点 \(Q\) が辺 \(AC\) 上を動くとする。このとき、\(\cos \angle PDQ\) の最大値を求めよ。
解答

問題1の解答

与えられた関数は \(f(x)=\frac{\log x}{\sqrt{x}}\) なので、商の微分公式を使って微分します。
$$f'(x)=\frac{(\log x)’ \cdot \sqrt{x}-\log x \cdot (\sqrt{x})’}{x}=\frac{\frac{1}{x}\cdot \sqrt{x}-\log x \cdot\frac{1}{2\sqrt{x}}}{x}$$
$$=\frac{2-\log x}{2x\sqrt{x}}$$

さて、ここで \(f'(x)=0\) を解くのですね!
次に \(f'(x)=0\) つまり、
$$\frac{2-\log x}{2x\sqrt{x}}=0$$
を解く。

あっ!真数条件により \(x>0\) であることを忘れていました!
この範囲で解けばいいので続きは・・・
真数条件より \(x>0\) であることに注意して、
$$\frac{2-\log x}{2x\sqrt{x}}=0$$
$$\Longleftrightarrow 2-\log x=0$$
$$\Longleftrightarrow \log x=2$$
$$\Longleftrightarrow x=\mathrm{e}^{2}$$

\(f'(x)=0\) の解は一つ出てきたぞ。あとは \(x\) がこの値のとき極大値となるか極小値となるかという問題がありますが、増減表をかいて調べるのでしたね!

\(x>0\) に注意すると、
$$f'(x)=\frac{2-\log x}{2x\sqrt{x}}$$
の符号は分子の \(2-\log x\) の符号に一致するので、下のように増減表が書けます。
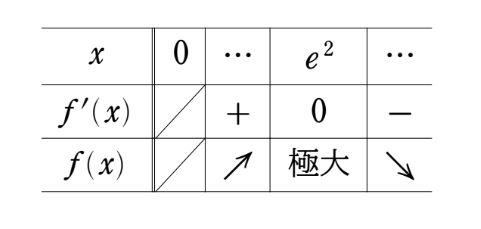
したがって、\(x=\mathrm{e}^{2}\) のとき極大値かつ最大値:
$$f(\mathrm{e}^{2})=\frac{\log \mathrm{e}^{2}}{\sqrt{\mathrm{e}^{2}}}=\frac{2}{\mathrm{e}}$$
となる。

素晴らしく完璧だ!微分して、方程式を解き、増減表を描くことで最大値がしっかり求められたな。この調子で問題2も頑張ってくれ。

はい、頑張ります!
問題2の解答

まずは \(\cos \angle PDQ\) を \(t\) を用いて表さなければなりませんね!

\(\triangle PDQ\) において余弦定理より、
$$\cos \angle PDQ=\frac{PD^{2}+QD^{2}-PQ^{2}}{2PD\cdot QD}\ \cdots ①$$
が成り立つので、\(PD\ ,\ QD\ ,\ PQ\) を \(t\) を用いて表すことを考える。

うーん、一番簡単に求められるのは辺 \(PD\) かな?
\(\triangle ABD\) は正三角形であり、点 \(P\) は辺 \(AB\) の中点であるから、
$$PD=AD\cdot \sin \frac{\pi}{3}=\frac{\sqrt{3}}{2}$$

よし、次は \(QD\) を求めます!
\(\triangle AQD\) において、余弦定理から
$$QD^{2}=AD^{2}+AQ^{2}-2AD\cdot AQ\cos \angle DAQ$$
$$=1^{2}+t^{2}-2\cdot 1\cdot t\cdot \cos \frac{\pi}{3}=t^{2}-t+1$$
\(QD>0\) より、\(QD=\sqrt{t^{2}-t+1}\)

よし、順調だぞ。最後に \(PQ\) を求めよう!
\(\triangle APQ\) において、余弦定理から
$$PQ^{2}=AP^{2}+AQ^{2}-2AQ\cdot AQ\cos \angle PAQ$$
$$=\left(\frac{1}{2}\right)^{2}+t^{2}-2\cdot \frac{1}{2}\cdot t\cdot \cos \frac{\pi}{3}=t^{2}-\frac{t}{2}+\frac{1}{4}$$
\(PQ>0\) より、\(PQ=\sqrt{t^{2}-\frac{t}{2}+\frac{1}{4}}\)

ふう、これで三辺を \(t\) を用いて表すことができたので\(\cos \angle PDQ\) を \(t\) を用いて表せるぞ!
したがって、①より
$$\cos \angle PDQ=\frac{PD^{2}+QD^{2}-PQ^{2}}{2PD\cdot QD}$$
$$=\frac{\frac{3}{4}+(t^{2}-t+1)-\left(t^{2}-\frac{t}{2}+\frac{1}{4}\right)}{\sqrt{3}\cdot \sqrt{t^{2}-t+1}}$$
$$=\frac{-\frac{t}{2}+\frac{3}{2}}{\sqrt{3}\cdot \sqrt{t^{2}-t+1}}$$
$$=\frac{1}{2\sqrt{3}}\cdot \frac{3-t}{\sqrt{t^{2}-t+1}}$$
すなわち、
$$\cos \angle PDQ=\frac{1}{2\sqrt{3}}\cdot \frac{3-t}{\sqrt{t^{2}-t+1}}$$

ふう、ようやく表せました!
あとはこの関数を微分して、\(f'(x)=0\) を解いて、増減表を書いて最大値を求めます。
ここで、定数倍を除いて
$$f(x)=\frac{3-t}{\sqrt{t^{2}-t+1}}\ (0 \le x \le 1)$$
とおく。\(x\) で微分すると、
$$f'(x)=\frac{(3-t)’\cdot \sqrt{t^{2}-t+1}-(3-t)\cdot (\sqrt{t^{2}-t+1})’}{t^{2}-t+1}$$
ここで、\((\sqrt{t^{2}-t+1})’\) において、\(u=t^{2}-t+1\) とおくと合成関数の微分法より
$$(\sqrt{t^{2}-t+1})’=(\sqrt{u})’\cdot (t^{2}-t+1)’=\frac{1}{2\sqrt{u}}\cdot (2t-1)=\frac{2t-1}{2\sqrt{t^{2}-t+1}}$$
となるので、これを代入して
$$f'(x)=\frac{(3-t)’\cdot \sqrt{t^{2}-t+1}-(3-t)\cdot \frac{2t-1}{2\sqrt{t^{2}-t+1}}}{t^{2}-t+1}$$
$$=\frac{-\sqrt{t^{2}-t+1}-(3-t)\cdot \frac{2t-1}{2\sqrt{t^{2}-t+1}}}{t^{2}-t+1}$$

ここで分母分子に \(2\sqrt{t^{2}-t+1}\) をかけて、分子の分数の分母を払います。
$$=\frac{-2(t^{2}-t+1)-(3-t)\cdot (2t-1)}{2(t^{2}-t+1)^{\frac{3}{2}}}$$
$$=\frac{-2t^{2}+2t-2+2t^{2}-7t+3}{2(t^{2}-t+1)^{\frac{3}{2}}}$$
$$=\frac{-5t+1}{2(t^{2}-t+1)^{\frac{3}{2}}}$$
すなわち、
$$f'(x)=\frac{-5t+1}{2(t^{2}-t+1)^{\frac{3}{2}}}$$
\(0 \le x \le 1\) の範囲において \(f'(x)=0\) を解くと、\((分母)>0\) より \(x=\frac{1}{5}\) を得る。

\(0 \le x \le 1\) に注意すると、
$$f'(x)=\frac{-5t+1}{2(t^{2}-t+1)^{\frac{3}{2}}}$$
の符号は分子の \(-5t+1\) の符号に一致するので、下のように増減表が書けます
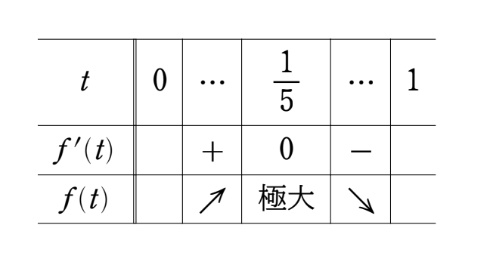
したがって、\(t=\frac{1}{5}\) のとき、\(f(t)\) は最大値:
$$f\left(\frac{1}{5}\right)=\frac{3-\frac{1}{5}}{\sqrt{\frac{1}{25}-\frac{1}{5}+1}}=\frac{14}{\sqrt{21}}=\frac{2\sqrt{21}}{3}$$
をとる。

最後に\(\frac{1}{2\sqrt{3}}\)をかけて
ゆえに、\(\cos \angle PDQ\) の最大値は、
$$\frac{1}{2\sqrt{3}}\cdot \frac{2\sqrt{21}}{3}=\frac{\sqrt{7}}{3}$$

とても、大変でしたが何とかできました!
最初は計算が複雑すぎて何度も途中で止まってしまいましたが、何度もやり直してようやくできた感じです。

長く大変な計算だったがよくミスなくできたぞ!
はじめはそれでいいのだ。自分の力で解ききることが大切だからな。計算力は一朝一夕では身に付かないから、あせらず地道な努力を続けていくしかないぞ。

はい、普段の練習が大切だと思いました!

では、今日はここまでにしよう。今回で微分の話は一応終わりとなる。最も伝えたかった、微分を用いて最大値・最小値を求めるということは良く理解できたことだろう。微分の話は今後、『多変数』へと進んでいくことになる。ここまで学ぶと世の中のあらゆることを予測可能となるのだ。まだまだ先は長いが、一歩一歩着実に進んでいくことが大切だ。次回からは、改めて第1回から始まることになるだろう。準備のためしばらく待っていてほしい。

分かりました。楽しみに待っています。今日もありがとうございました!






コメント