微分の意義

やあ、こんにちは。今日は微分の意義について学ぼう。

はい!よろしくお願いします。


はい、大丈夫です。

この接線の傾きに注目することによって色々なことが分かってくるのだ。さて、一般にある関数が与えられたとき、その関数の最大値(max)、最小値(min)を求めることは重要な問題となる。そして、maxとminを求めるための強力な道具となるのが微分なのだ!簡単な具体例を通してこのことを見ていくとしよう。とりあえず \(f(x)=x^{2}-6x+7\) の最小値を求めてみてほしい。

はい、これは2次関数なので平方完成の一手ですね!
2次関数の最小値

$$f(x)=x^{2}-6x+7=(x-3)^{2}-2$$
となるので、グラフは下図のようになる。よって、最小値は \(x=3\) のとき \(-2\) となる。
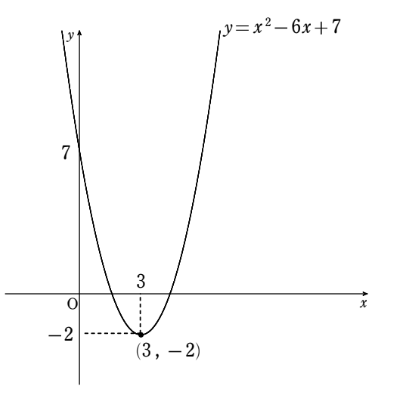
\((導関数)=0 \) なる方程式について


うむ、そうなるな。次にあえて微分を利用してこの関数の最小値を求めてみよう。まず、微分するとその導関数は、\(f'(x)=2x-6\) となることはいいよな?では、『 (導関数)=0 』とおいた方程式を解くとどうなる?

\(2x-6=0\) なので、もちろん \(x=3\) となります。

この解が上で求めた最小値を与える \(x\) の値になっていることに気づかないかい?

あれっ?本当だ!
上で最小値は \(x=3\) のとき \(-2\) と求めました。
もちろん偶然の一致ということではないですよね?

これこそが微分がmaxとminを求めるための強力な道具となることの理由なのだ!つまり、maxとminの問題は、微分することによって『方程式を解く問題』に帰着できるのだ!

これは一体どういうからくりなんでしょう?
からくりについて


ふふふ、とてもシンプルな理由だよ。導関数は接線の傾きを与えてくれる関数だったろう?なので接線の傾きに注目してごらん。下図のように \(x=3\) を境に接線の傾きが負から正に変化しているだろう。そして、\(x=3\) においては接線の傾きは \(0\) となっている。
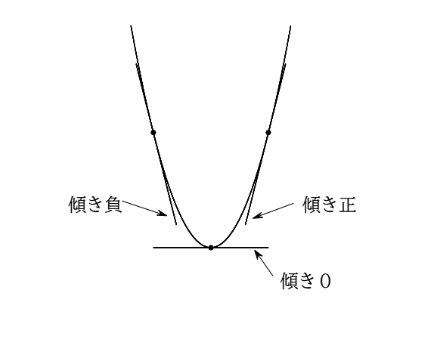

つまり、接線の傾きが負のとき元の関数は減少し、接線の傾きが正のとき元の関数は増加するといえるのだ。そして、接線の傾きが負から正、あるいは正から負に変化するとき、接線の傾きが0になるということもいえる。

そうか! (導関数)=0 の解は、言い換えると接線の傾きが \(0\) になるような \(x\) の値だから、今回のグラフが下に凸であることを考えると、まさに最小値を与える『谷底』にあたる部分の \(x\) の値を求めることになるのですね!

その通りだ!同じことは上に凸なグラフに対してもいえるのだ!
つまり、 (導関数)=0 の解は最大値を与える『山の頂上』にあたる部分の \(x\) の値を求めることになるのだ。

これは目から鱗という感じですね!平方完成するよりも簡単にかつ早く最小値や最大値が求められますね!例えば \(f(x)=-2x^{2}+8x-10\) の最大値は、微分して \(f'(x)=-4x+8\) となるから \(x=2\) で最大値 \(-2\) となります!

うむ、この考えを応用すれば次のような3次関数の最大値と最小値も求められるようになるのだ!例えば \(f(x)=2x^{3}-3x^{2}-12x-5\ (-2 \le x \le 4)\) について考えてみよう。これは、平方完成はできないから微分に頼らざるを得ないな。

はい、微分して (導関数)=0 を解くのでしたよね!やってみます。
3次関数のmax・min問題

\(f(x)=2x^{3}-3x^{2}-12x-5\) を微分して、
$$f'(x)=6x^{2}-6x-12=6(x^{2}-x-2)=6(x-2)(x+1)$$
より、\(f'(x)=0\) を解くと、\(x=-1\ ,\ 2\) を得る。

とりあえず、\(f'(x)=0\) を解いて、\(x=-1\ ,\ 2\) を得ましたが、どちらが最大値、あるいは最小値を与えるのかという問題が出てきました。

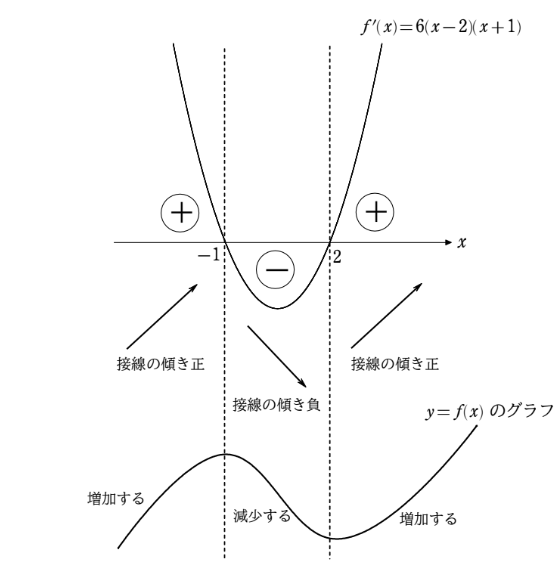
うむ当然の疑問だな!そういうときは、導関数のグラフを描いてみるんだよ。つまり、\(f(x)=6(x-2)(x+1)\) のグラフを描いてみると下図のようになるだろう?ここで、図に書かれている+とーの記号は、\(f'(x)\) の符号を表している。
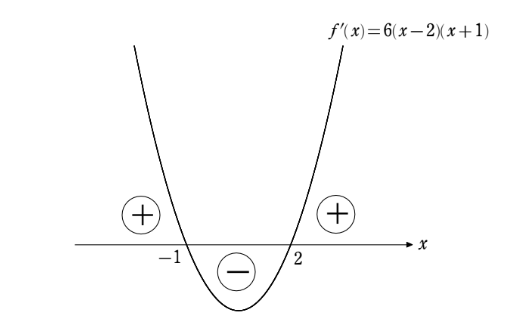

グラフより、\(x<-1\) のとき \(f'(x)>0\)、\(-1<x<2\) のとき \(f'(x)<0\)、\(2<x\) のとき \(f'(x)>0\) となっているから、これすなわち接線の傾きが下図のようになっていることに他ならない。ここまでよろしいか?
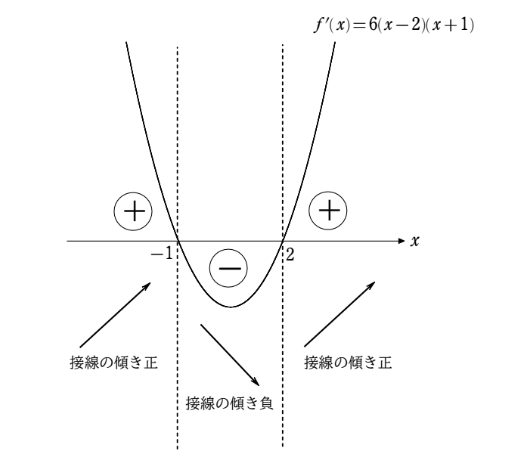

はい、ということは元の関数 \(y=f(x)\) のグラフは\(x<-1\) のとき増加し、\(-1<x<2\) のとき減少し、\(2<x\) のときまた増加する、ということですね!よって、\(x=-1\) で『山の頂上』となり、\(x=2\) で『谷底』になることが分かります!したがって、\(x=-1\) で最大値をとり、\(x=2\) で最小値を取る、ということですね!
増減表について


うーん、惜しい!
\(x=-1\) で『山の頂上』になって、\(x=2\) で『谷底』になるというところまでは正しいのだが、これらがそれぞれ最大値、最小値となるのは本当にそうだろうか?そのことを確認するために、増減表というものを書いてみよう。下図を見てほしい。
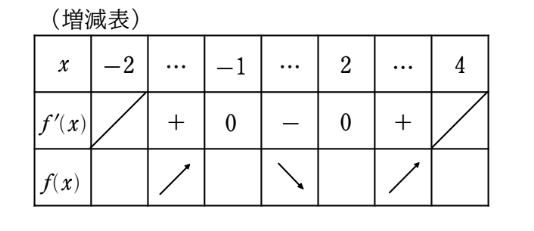

増減表は、上に描いた三つのグラフ \(y=f'(x)\) と接線の傾きと \(y=f(x)\) のグラフをコンパクトにまとめただけだということに注目してほしい。さて、ヒロトには表の最後の行を計算して埋めてもらおうか。そうすると、おのずと最大値、最小値が決定されるだろう。

ああ、そうか!定義域の端の値、\(x=-2\) と \(x=3\) のときの値も考えなくてはいけないのですね!では、ノートに計算してみます。
$$f(-2)=-16-12+24-5=-9$$
$$f(-1)=-2-3+12-5=2$$
$$f(2)=16-12-24-5=-25$$
$$f(4)=128-48-48-5=27$$
となるので、増減表は下のようになる。
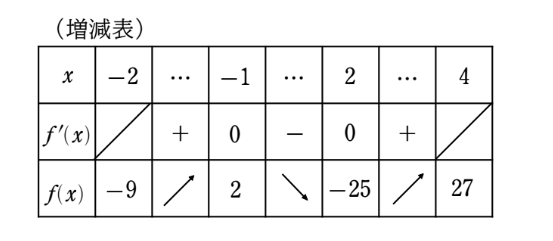

よって、最小値は
$$x=2のとき-25$$
最大値は
$$x=3のとき27$$
となります。最小値は『谷底』になりましたが、最大値は山の頂上ではなく右端の \(x=3\) においてなることが分かりました。

その通りだ!2次関数の時は、山の頂上が最大値、谷底が最小値にそのままなるから気にしなくてよかったが、3次以上になると話は変わってくるから、しっかり増減表を書いて調べなくてはならないのだ。ここで、数学では山の頂上と谷底に対応する値のことを『極大値』、『極小値』と言うから覚えておいてくれ。ちなみに極大値と極小値をまとめて極値ともいうぞ。さて、増減表を用いて下のように元の関数のグラフの概形も描くことができる。
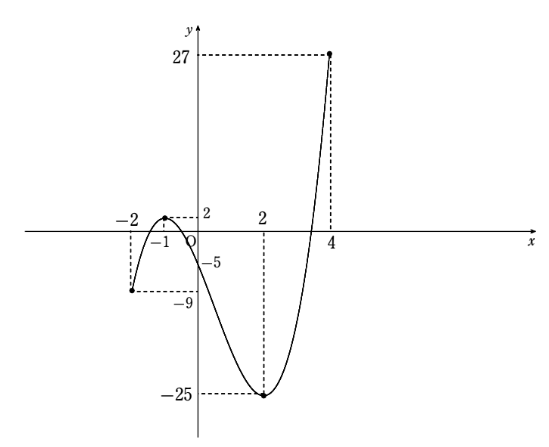

微分して導関数を調べることで色々なことが分かり、元の関数のグラフまで書けるようになったことは驚きですね!

その通りだな。
今回の微分を利用して最大値・最小値を求める方法は、3次関数に限らずこれまで微分してきたすべての関数に対して使える方法なのだ。詳しくは次回にゆずることにしよう。さて、今日は微分の意義について話をしてきたが、伝えたかったことを一言でまとめると、
$$『(導関数)=0\ を解くことで最大値・最小値を求めることができる』$$
ということだ。これは今後キーワードになってくるから忘れずにいてほしい。

はい!本当にすごいと思ったので絶対に忘れることはないと思います。

うむ、では今回はここまでにしよう。次回は最大値・最小値に関する練習問題をやりたいと思う。実際に大学入試に出された問題を取り扱うからそのつもりでいてくれ。では、今日もお疲れさん。

はい、ありがとうございました!





コメント