対数関数の定義

やあ、こんにちは。前回は何とか指数関数の微分を完了させたので、今回はいよいよ対数関数の微分についてやっていこう!

はい、よろしくお願いします!

初めに対数関数 \(f(x)=\log_a x\) の定義から確認しよう。\(a\) については指数関数のときと同じく底(てい)と呼び、また指数関数のときと同じ理由により \(1\) ではない正の整数である。そして、対数 \(\log_a x\) の定義とは、
$$a^{\log_a x}=x \ \cdots (\star)$$
を満たす実数だということだ。

はい、指数関数と対数関数は互いに逆関数の関係にもあることも勉強済みです。
指数関数に帰着させる

対数関数を微分するためには、指数関数のときと同様にやはり、合成関数の微分が必要となる。指数関数と対数関数の橋渡しとなってくれるのが \((\star)\) なのだ。まずは、\(y=\log_a x\) の両辺を \(a\) の肩に乗せることから始めてみよう。

はい、両辺を \(a\) の肩に乗せてもイコールであることには変わりないから・・・
\(f(x)=\log_a x\) の両辺を \(a\) の肩に乗せて、\((\star)\) を用いると、
$$a^{f(x)}=a^{\log_a x}\ \Longleftrightarrow\ a^{f(x)}=x\ となる。$$

うむ、そうなるな。ここで、今導いた \(a^{f(x)}=x\) を見て何か気づかないかい?特に左辺を見てどうだ?前回やったあれを思い出さないかい?
合成関数の微分の出番


あ、そうか!左辺の \(a^{f(x)}\) は合成関数になっています!
つまり、指数関数に \(f(x)\) が代入された形になっています!ということは合成関数の微分公式が使えるということですね!

よく気づいたな、その通りだ!しっかりつながってきただろう?
今回は \(a^{f(x)}=x\) の両辺を \(x\) で微分して進めてみよう!

はい!では続けていきます。
\(f(x)=\log_a x\) の両辺を \(a\) の肩に乗せて、\((\star)\) を用いると、
$$a^{f(x)}=a^{\log_a x}\ \Longleftrightarrow\ a^{f(x)}=x\ となる。$$
両辺を \(x\) で微分すると、左辺は
$$g(x)=a^{x}\ ,\ f(x)=f(x)\cdots(そのまま)\ とおくと、g(f(x))=a^{f(x)}\ $$
という合成関数になっているから、合成関数の微分より、
$$\left\{g(f(x))\right\}’=g'(u) \cdot f'(x)=(a^{u})’\cdot f'(x)$$
と書ける。\((a^{u})’=a^{u}\log a\) であったからこれを代入して、
$$(左辺)=a^{u}\log a \cdot f'(x)\ となる。$$
一方、右辺はもちろん \(x’=1\) であるから、両辺合わせて、
$$a^{u}\log a \cdot f'(x)=1$$
を得る。我々は \(f'(x)\) を求めるのが目的であったから、 \(f'(x)\) について解いて、
$$f'(x)=\frac{1}{a^{u}\log a}\ となる。$$

出来ました!

素晴らしいぞ!でも一つ忘れていることがあるぞ。自分で気付けるかい?

忘れていること・・・あっそうか! \(u\) のままになってるや!
\(u=f(x)\) と戻さないといけなかったんですね?
$$a^{u}=a^{f(x)}=a^{\log_a x}=x\ より、$$
$$f'(x)=\frac{1}{x\log a}$$
となります!

完璧だ!どうだ?合成関数の微分公式のおかげでスムーズにできただろう!
これで対数関数の微分法は完了した!
$$(\log_a x)’=\frac{1}{x\log a}$$
※\(右辺分母の \log a の底は自然対数 \mathrm{e}であることに注意\)
特に底が \(\mathrm{e}\) の場合、\(\log \mathrm{e}=1\) であるから、
$$(\log x)’=\frac{1}{x}$$
となることに注意!

指数関数のときににいろいろ頑張ったおかげであっという間に終わりました!
先生、早く終わったのでまたいくつか練習問題をくれませんか?

よーし、いいだろう!前回の指数関数の問題もついでに出してやろう。

はい、ありがとうございます!
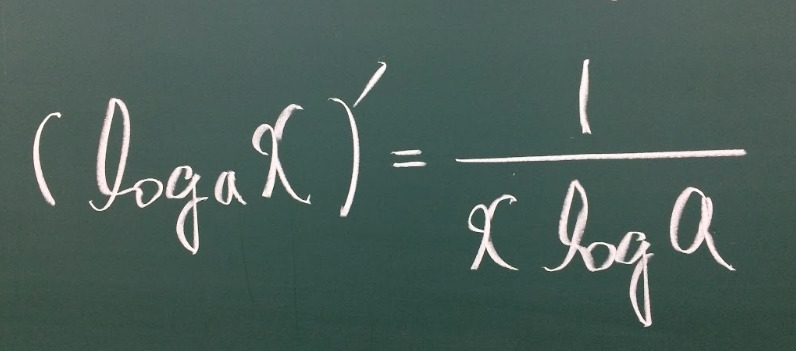
練習問題

問題
次の関数たちを微分せよ。
(1) \(f(x)=3^{x}\)
(2) \(f(x)=3^{-x}\)
(3) \(f(x)=\mathrm{e}^{-x^{2}}\)
(4) \(f(x)=\log_5 x\)
(5) \(f(x)=\log_{\frac{1}{5}} x\)
(6) \(f(x)=\log (x^{2})\)
解答
(2) \(3^{-x}=(3^{-1})^{x}=\left(\frac{1}{3}\right)^{x}\) と見ると、公式よりそのまま
$$f'(x)=\left\{\left(\frac{1}{3}\right)^{x}\right\}’=\left(\frac{1}{3}\right)^{x}\cdot\log \left(\frac{1}{3}\right)=-3^{-x}\log 3$$
(3) \(g(u)=\mathrm{e}^{u}\ ,\ f(x)=-x^{2}\) と置くと、これは合成関数:
$$g(f(x))=\mathrm{e}^{-x^{2}}$$
表されるので、合成関数の微分公式より
$$f'(x)=(\mathrm{e}^{u})’\cdot(-x^{2})’=\mathrm{e}^{u}\cdot(-2x)=-2x\mathrm{e}^{-x^{2}}$$
(4) 公式より、そのまま
$$f'(x)=\frac{1}{x\log 5}$$
(5) 公式より、そのまま
$$f'(x)=\frac{1}{x\log (\frac{1}{5})}=-\frac{1}{x\log 5}$$
(6) \(\log (x^{2})=2\log x\) であることと、底が \(\mathrm{e}\) であることに注意して、
$$f'(x)=(2\log x)’=2\cdot\frac{1}{x\log \mathrm{e}}=2\cdot\frac{1}{x}=\frac{2}{x}$$

出来ました!微分公式と、指数関数と対数関数の基本的な性質のみを使うことによって微分がスラスラできるようになるのは気持ちいいですね!微分の定義式から計算するのはとても大変だったのでなおさらそう思います。

そうだろう!公式は証明するまでが大変だが、一度示してしまえばその恩恵は多大だということだな。さて、これで主要な関数たちの微分についてはすべて完了したぞ!よくここまで頑張ったな!次回はこれまでの総まとめ問題演習を実施したいと思う。もはや高校数学に出てくるどんな関数も微分できるようになっているぞ!では、今日はここまでにしよう。お疲れさん。

はい!次回に備えてしっかり復習してきます。
今日もありがとうございました!


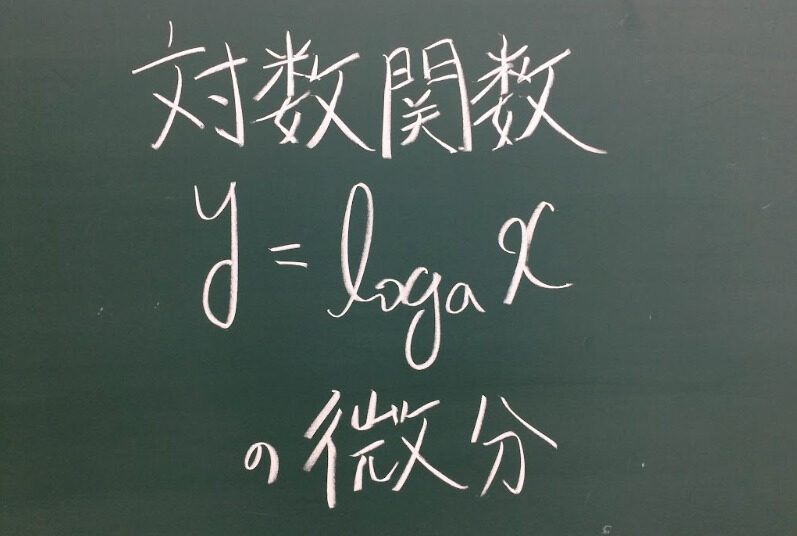



コメント