微分の線形性

やあ、こんにちは。今回は微分の性質について学んでいこう!

微分の性質については前回の最後に一つ見つけました!
それは、『微分は次元を一つ下げる』という性質です。

うむ、それはそれでとても大事な性質なのだが、今回学ぶ『微分の性質』とは
微分の計算法則についてのものだ。その名も『微分の線形性』についてだ。

微分のセンケイセイですか?

ああ、具体例を用いて説明しよう。まずは、前回学んだ方法で関数 \(f(x)=x^{3}+x^{2}+x+1\) を微分してみてくれ。

はい、いつも通りノートにやります。
$$f^{\prime}(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$$
$$=\lim_{h \to 0}\frac{\{(x+h)^{3}+(x+h)^{2}+(x+h)+1\}-(x^{3}+x^{2}+x+1)}{h}$$
$$=\lim_{h \to 0}\frac{(x^{3}+3x^{2}h+3xh^{2}+h^{3}+x^{2}+2hx+h^{2}+x+h+1)-x^{3}-x^{2}-x-1}{h}$$
$$=\lim_{h \to 0}\frac{3x^{2}h+3xh^{2}+h^{3}+2hx+h^{2}+h}{h}$$
$$=\lim_{h \to 0}(3x^{2}+3xh+h^{2}+2x+h+1)=3x^{2}+2x+1$$
$$よって、(x^{3}+x^{2}+x+1)^{\prime}=3x^{2}+2x+1$$

ふう、かなり大変でしたが何とかできました!

うむ、正解だ!頑張ったな。ところで、前回の最後にやった4問の結果と見比べて何か気づかないかい?

ん?えーと、前回の問題4問の結果はと・・・
$$(c)^{\prime}=0\ \ ,\ \ (x)^{\prime}=1\ \ ,\ \ (x^{2})^{\prime}=2x\ \ ,\ \ (x^{3})^{\prime}=3x^{2}$$

・・こうでしたね。ああ、そういうことか!

ふふ、気づいたようだな、微分は分配できるという性質に!

はい!つまりこういうことですね?
\(f^{\prime}(x)=(x^{3}+x^{2}+x+1)^{\prime}=(x^{3})^{\prime}+(x^{2})^{\prime}+x^{\prime}+1^{\prime}=3x^{2}+2x+1\)

まさにそういうことだ!更に、定数倍は無視できるという性質もある。例えば、
\((3x^{2})^{\prime}=3\cdot(x^{2})^{\prime}=3\cdot(2x)=6x\) とできる。\((3x^{2})^{\prime}=3^{\prime}\cdot(x^{2})^{\prime}\)とはならないのだ。

なんか不思議な性質ですね!

この分配できてかつ定数倍は無視できるという性質を『線形性』と言うのだ。公式風に書くと次のようになる。
$$\{f(x)+g(x)\}^{\prime}=f^{\prime}(x)+g^{\prime}(x)\ \cdots\ ①$$
$$\{af(x)\}^{\prime}=af^{\prime}(x)\ \ (a は定数)\ \cdots\ ②$$

項ごとに微分できるということは、計算量を劇的に減らしてくれる方法なのですね!

そういうことだ。しかし、なぜ微分は線形性を持つのだろうか?
この疑問にはまだ答えていないな。つまり、まだ証明していない。

確かに!上の例はたまたま成り立ったということかもしれないですよね?

ああそうだ。今後、微分に関する性質は多く出てくるが、その証明は全て『微分の定義式』から証明できるのだ!これは、微分の定義式の奥深さに触れることはもとより、『数学理論の構築』というのがどのようなものなのかを我々に教えてくれるのだ。

微分の線形性の証明

証明する前に、『微分の定義式』もう一度書いてみてくれ!
この式がすべてなんだ。

はい、こうなります。
微分の定義式:$$f^{\prime}(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$$

よし、いいぞ。では、はじめに線形性の性質①を証明しよう。
\(\{f(x)+g(x)\}^{\prime}=f^{\prime}(x)+g^{\prime}(x)\ \cdots\ ①\)の証明

はじめに、二つの関数 \(f(x)\ ,\ g(x)\) の和 \(f(x)+g(x)\) も、もちろん関数であるからこれを \(F(x)\) という新しい関数として定義する。すると、左辺の \(\{f(x)+g(x)\}^{\prime}\) は \(F^{\prime}(x)\) と書けるのでとても見通しが良くなるのだ。これは、よく使う重要なテクニックだから覚えておいてくれ。すると、左辺は定義より次のように変形できる。
$$F^{\prime}(x)=\lim_{h \to 0}\frac{F(x+h)-F(x)}{h}$$

後は定義に従って右辺をコツコツ計算していけば示すべき式が自然と出てくるのだ。最初だから私がやってみよう。
$$F^{\prime}(x)=\lim_{h \to 0}\frac{F(x+h)-F(x)}{h}$$
$$=\lim_{h \to 0}\frac{\{f(x+h)+g(x+h)\}-\{f(x)+g(x)\}}{h}$$
$$=\lim_{h \to 0}\frac{\{f(x+h)-f(x)\}+\{g(x+h)-g(x)\}}{h}$$
$$=\lim_{h \to 0}\{\frac{f(x+h)-f(x)}{h}+\frac{g(x+h)-g(x)}{h}\}$$
$$=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}+\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}$$
$$=f^{\prime}(x)+g^{\prime}(x)$$

わー本当ですね!自然と示すべき式が出てきましたね。

ふふ、そうだろう。
まあ、ちょっとうるさいことを言うと最後から3番目の式を計算するとき \(\lim_{h \to 0}\) を『分配』したのだが、これができるためには \(f(x)\) と \(g(x)\) がともに微分可能な関数であることが必要だ。でも、我々が扱う関数は『微分可能な関数』ばかりだから今後も \(\lim_{h \to 0}\) は分配できると考えていいぞ。

ということは微分不可能な関数もあるということですか?

するどいな、その通りだ。理論的には部分的に微分できない関数やすべての点で微分できない関数が存在するのだ(下図参照)。しかし、さっきも言ったが今はそれほど気にすることはないぞ。では続けて線形性の性質②を証明しよう。
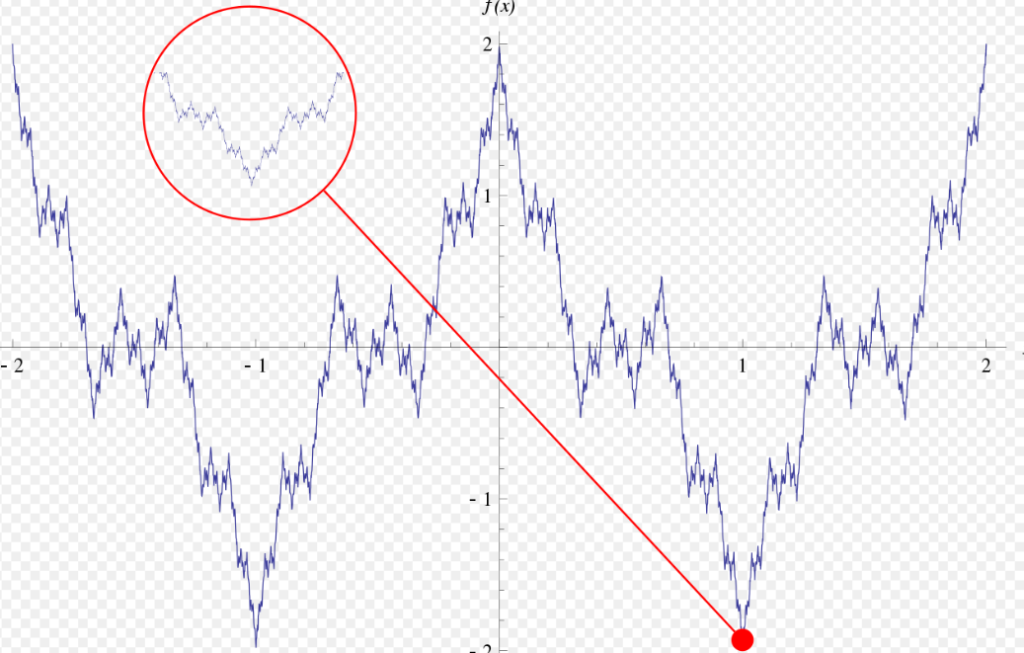
\(\{af(x)\}^{\prime}=af^{\prime}(x)\ \cdots\ ②\) の証明

では、今度はヒロトにやってもらおうか!

はい!任せて下さい。
さっきと同じように \(F(x)=af(x)\) とおいて定義にしたがって計算します。
$$F(x)=\lim_{h \to 0}\frac{F(x+h)-F(x)}{h}$$
$$=\lim_{h \to 0}\frac{af(x+h)-af(x)}{h}$$
$$=\lim_{h \to 0}\frac{a\{f(x+h)-f(x)\}}{h}$$
$$=a\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$$
$$=af^{\prime}(x)$$

できました!定数 \(a\) を外に出すことがポイントですね。

素晴らしい!正解だ。
これで、微分の線形性について証明が完了したのでこれからはこの性質をどんどん使っていこう!

微分の定義式の奥深さが少し分かりました。

そうか!しかし、驚くのはまだ早いぞ。次回から学ぶ『微分公式』の全てがこの微分の定義式から生まれるのだ!まさに母なる式なのだ。まあ、今回はこの辺にして最後に練習問題をやって終わることにしよう。

はい!そうしましょう。

以下の問題は、前回の問題の結果である、
$$c^{\prime}=0\ \ ,\ \ x^{\prime}=1\ \ ,\ \ (x^{2})^{\prime}=2x\ \ ,\ \ (x^{3})^{\prime}=3x^{2}$$
を使っていいぞ!ぜひ線形性を用いて、エレガントに計算してくれ!

練習問題(微分の線形性)
問題
次の関数を微分せよ。
(1) \(f(x)=2x^{2}+3x+1\)
(2) \(f(x)=3x^{3}-2x^{2}+x+4\)
解答
$$よって、f^{\prime}(x)=4x+3$$
$$よって、f^{\prime}(x)=9x^{2}-4x+1$$

すごい!『線形性』のおかげで計算がとても簡単になりましたね!

そうだろう?『線形性』の威力というものがよく分かったみたいだな!
さて、第4回はここまでにしよう。次回は『微分公式』を紹介するぞ。

はい、今日はありがとうございました!
ティーブレイク
今回出てきた『線形性』という性質は数学の世界においてとても重要な性質の一つだ。数学の世界で、重要とされる三大性質は、『存在性』、『一意性』そして『線形性』である。
数学における重要な演算は『微分・積分』を始めとして線形性を満たす。この重要な線形性に焦点を当てた数学の分野が『線形代数学』なのだ。線形代数は現代、多くの分野に応用されている最重要分野である。単純な性質から豊かな数学理論が構築され、それが現実に応用されていくことは、まさに数学の醍醐味の一つである。







コメント