指数関数の微分

こんにちは、今回は指数関数の微分について学んでいこう。
今回は今までのようにスムーズにはいかないことを最初に言っておこう。

う、そうなんですね。
とりあえず今日もよろしくお願いします!
指数関数の定義

さて、まず指数関数の定義についてだが正確に知っているかな?

はい、教科書で予習済みです。
\(y=a^{x}\) という形をした関数で、\(a\) は \(1\) 以外の正の定数です。

うむ、完璧だ!ちなみに、\(a\) が \(1\) 以外の正の定数と定められている理由は分かるかな?

えーと、\(a=1\) の場合は \(y=1^{x}=1\) という定数関数になって、特に指数関数として扱わなくてよいからです。でも、\(a\) が負の場合がなぜ除外されているのかはあまり考えたことがなかった気がします。

\(a=1\) の場合の理由はその通りだ。\(a\) が負の場合がなぜ除外されているのかについては、例えば \(a=-1\) の場合を考えてみよう。このとき、\(y=(-1)^{x}\) と書けるだろう?そして、\(x\) は実数全体を動くので \(x=\frac{1}{2}\) の場合、関数の値はどうなるだろうか?

えーと、
$$y=(-1)^{\frac{1}{2}}=\sqrt{-1}$$
となります。ああ、ルートの中が負になってしまいました!これは確か虚数というもので、実数ではないですね?

そのとおり!\(a\) が負の場合、このように関数の値が虚数、もっと一般に複素数になってしまうので、これではまずいというわけなんだ。
数学の世界には複素関数論という複素変数を用いて微分などを考える分野があるのだが、それは我々が学ぶ内容とは関係性がないのだ。我々が扱う関数はすべて実数変数かつ実数値関数で十分なのだ。

なるほど、だから \(a\) が負の場合は除かれるのですね。よく分かりました!
微分の定義式からスタート

定義について完璧になったところで、さっそく指数関数を微分してみてくれ。何から始めるかはもう言わなくても大丈夫だな?

はい!微分の定義式からスタートですね!
では始めます。
$$f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}=\lim_{h \to 0}\frac{a^{x+h}-a^{x}}{h}$$
指数法則により、\(a^{x+h}=a^{x}a^{h}\) となるので、\(a^{x}\) でくくって、
$$(上式)=\lim_{h \to 0}\frac{a^{x}a^{h}-a^{x}}{h}=\lim_{h \to 0}\frac{a^{x}(a^{h}-1)}{h}$$
$$x だけの関数は \lim_{h \to 0} の影響を受けないので \lim_{h \to 0} の外に出して、$$
$$(上式)=a^{x}\cdot\lim_{h \to 0}\frac{a^{h}-1}{h}$$

先生、見慣れない極限、
$$\lim_{h \to 0}\frac{a^{h}-1}{h}$$
が出てきました。この値が求められれば完成するのですが・・・

いいぞ、ここまでは完璧だ!微分の定義式の扱いに本当に慣れてきたみたいだな。\(x\) だけの関数を \(\lim_{h \to 0}\) の外に出すあたりなんか特に上手だぞ。さて、指数関数と対数関数の微分が難しいのはここからなんだ。一つ一つ着実に進んでいこう。上の計算の結果、
$$\lim_{h \to 0}\frac{a^{h}-1}{h}$$
という極限値を計算することが必要になった。ところで、この極限値は何を意味するのかよく考えてみて欲しい。ヒントは \(a^{0}=1\) だ。
初見の極限値

ヒント通り、分子の \(1\) を \(a^{0}\) に書き換えて・・
$$\lim_{h \to 0}\frac{a^{h}-a^{0}}{h}\ \cdots\ ①と書ける。$$

うーん、何も見えてきませんね・・・

もちろん最初は誰だってそうさ。
では、次のヒントだ。次に、\(f(x)=a^{x}\) の \(x=0\) における微分係数の定義式を書いてみてくれ。微分係数については久しぶりに出てきたので必要であれば振り返ってみていいぞ!

はい、\(x=0\) における微分係数 \(f'(0)\) は・・・
\(f(x)=a^{x}\) の \(x=0\) における微分係数は、
$$f'(0)=\lim_{h \to 0}\frac{f(0+h)-f(0)}{h}=\lim_{h \to 0}\frac{a^{h}-a^{0}}{h}$$

あ!上の①と一致しました!
極限値の意味

気づいたみたいだな!そして、微分係数が意味するのは、グラフの世界において何だった?

確か、その点における接線の傾きです!
第2回で学びました。

その通り!ということは、問題になっている極限値、
$$\lim_{h \to 0}\frac{a^{h}-1}{h}$$
の意味は \(f(x)=a^{x}\) の \(x=0\) における接線の傾きだということになるのだ。ここまでよろしいか?

はい、大丈夫です!でも意味は分かっても実際の値が分からなくて困っているのです。

まあ、あせらずに行こう。いいかい?ちょっと下の図を見てくれ。これは、\(a>1\) の場合の\(y=a^{x}\) のグラフを描いたものだ。すると、\(x=0\) における接線の傾きはとりあえず正の値ということは予想がつくだろう?


はい、確かに!\(a>1\) の場合の\(y=a^{x}\) はずっと増加し続けるのでそうなると思います。ということは求める極限値も正の数ということになりますよね?

そういうことになるな。ここからはちょっとイメージしてほしいのだが、\(a\) の値が \(1\) に近づくと \(y=a^{x}\) は定数関数 \(y=1\) に近づくので \(x=0\) における接線の傾きはもちろん \(0\) になっていくだろう?そして、\(a\) の値がとても大きな正の数になると \(x=0\) における接線の傾きはとても急になるだろう?
どうだ?イメージできるか?下図も参考にしてみてくれ。
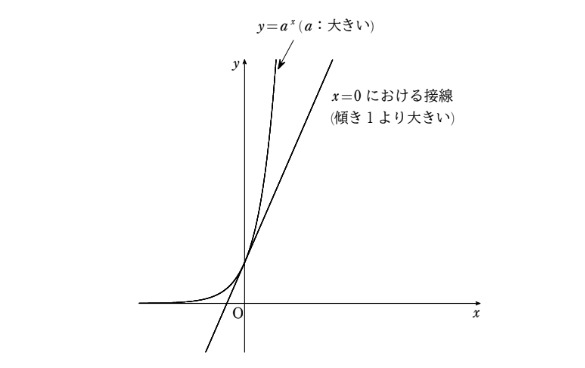

はい、そうなると思います。ただ、\(a\) の値が変化しても、点 \((0\ ,\ 1)\) を通ることは変わりませんよね?
自然対数の底
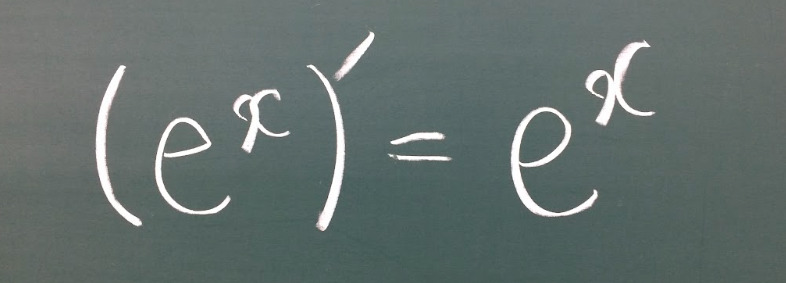

うむ、その通りだ。ということはだ、いいかい?ということは、\(a\) がある正の数のときに\(x=0\) における接線の傾きがちょうど \(1\) になるときがあるだろう?

はい!接線の傾きが \(0\) から徐々に増えていくのですから、ある時点で接線の傾きが \(1\) となるときがあるでしょうね!
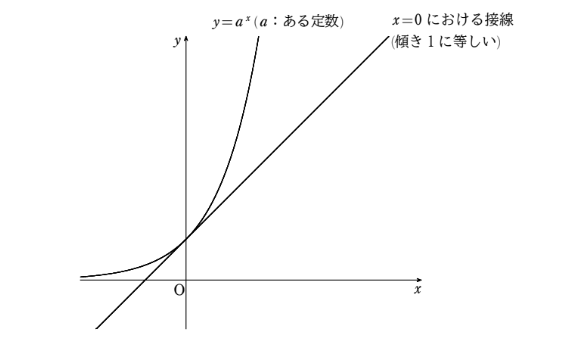

そうだ!では、その存在する正の数を \(\mathrm{e}\) と表すことにしよう!
この数を数学では自然対数の底と呼ぶのだ。すなわちその定義は、
$$\lim_{h \to 0}\frac{\mathrm{e}^{h}-1}{h}=1$$
というわけだ。これで、とりあえず \(a=\mathrm{e}\) の場合は問題は解決したな。ヒロトよ、ノートにまとめてみてくれ。

はい!\(a=\mathrm{e}\) の場合ですね!
\(a=\mathrm{e}\) の場合:
$$f'(x)=(\mathrm{e}^{x})’=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}=\lim_{h \to 0}\frac{\mathrm{e}^{x+h}-\mathrm{e}^{x}}{h}$$
指数法則により、\(\mathrm{e}^{x+h}=\mathrm{e}^{x}\mathrm{e}^{h}\) となるので、\(\mathrm{e}^{x}\) でくくって、
$$(上式)=\lim_{h \to 0}\frac{\mathrm{e}^{x}\mathrm{e}^{h}-\mathrm{e}^{x}}{h}=\lim_{h \to 0}\frac{\mathrm{e}^{x}(\mathrm{e}^{h}-1)}{h}$$
$$x だけの関数は \lim_{h \to 0} の影響を受けないので \lim_{h \to 0} の外に出して、$$
$$(上式)=\mathrm{e}^{x}\cdot\lim_{h \to 0}\frac{\mathrm{e}^{h}-1}{h}=\mathrm{e}^{x}\cdot 1=\mathrm{e}^{x}$$
$$つまり、(\mathrm{e}^{x})’=\mathrm{e}^{x}\ \ が成り立つ。$$

結果的に \(y=\mathrm{e}^{x}\) という指数関数は、微分しても変化しない関数という結論になりました!こんなことってあるんですね?

ああ、数学の世界で最重要な関数に我々は今出会ったのだ!
指数関数と対数関数の微分は、この関数が中心的な役割を担ってなされるのだ。
さあ、今回はとても重要な内容なった。けっこう重い内容になったのでとりあえず今日のところはここまでにしよう。お疲れさん。

はい、しっかり復習しておきます。
今日もありがとうございました!






コメント