最重要な関数たち

やあ、こんにちは。今回は数学の世界において、最重要な関数たちを微分していこう。

はい、よろしくお願いします。
最重要な関数とはどんなものですか?

どれも高校の教科書に出てくるもので、以下の関数たちだ。
$$f(x)=\sin x\ ,\ f(x)=\cos x\ ,\ f(x)=\tan x$$
$$f(x)=a^{x}\ (aは正の定数)\ ,\ f(x)=\log x$$

三角関数、指数関数、そして対数関数ですね。どれも教科書に出てくる有名な関数ですね!

うむ、これら関数の定義について、もし不安なら教科書などを読んでしっかり確認しておいてほしい。

はい、大丈夫です。確認してきました!

\(f(x)=\sin x\) の微分

よし、感心感心!
では、さっそく \(f(x)=\sin x\) の微分を考えて行こう!
微分公式の類はすべて定義式が与えてくれると言ったことは覚えているかな?
まずは定義式に従って計算をスタートしてみよう!

はい、頑張ります!
$$f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}=\lim_{h \to 0}\frac{\sin (x+h)-\sin x}{h}$$

大体いつもここで詰まるのです・・・

ははは、最初からスラスラできる方がおかしいってもんさ。
ヒントは加法定理だ!

あー加法定理は知っています。
$$\sin (x+h)=\sin x\cos h+\sin h\cos x$$
だったはず!これを代入すると・・・
$$\lim_{h \to 0}\frac{\sin (x+h)-\sin x}{h}=\lim_{h \to 0}\frac{(\sin x\cos h+\sin h\cos x)-\sin x}{h}$$
$$=\lim_{h \to 0}\frac{\sin x(\cos h-1)+\sin h\cos x}{h}$$
$$ここで、\lim_{h \to 0} を分配して、$$
$$=\lim_{h \to 0}\frac{\sin x(\cos h-1)}{h}+\lim_{h \to 0}\frac{\sin h\cos x}{h}$$
$$x だけの関数は \lim_{h \to 0} の影響を受けないので \lim_{h \to 0} の外に出して、$$
$$=\sin x\cdot\lim_{h \to 0}\frac{\cos h-1}{h}+\cos x\cdot\lim_{h \to 0}\frac{\sin h}{h}$$

とりあえずここまでできました!
$$\lim_{h \to 0}\frac{\cos h-1}{h}\ ,\ \lim_{h \to 0}\frac{\sin h}{h}$$
という見慣れない極限値が出てきました。
$$\lim_{h \to 0}\frac{\sin h}{h}=1\ について$$

うむ、\( \lim_{h \to 0} \) の扱い方に慣れてきたようだな。練習を怠らなかった証拠だ、感心感心。さて、ここから先は新しい知識を必要とするのだ。以前第2回で、有名な極限値の例として、
$$\lim_{h \to 0}\frac{\sin h}{h}=1$$
を紹介したことを覚えているかい?

はい、極限値は単に \(0\) を代入するのとは違うという説明のときに見ました。

素晴らしい記憶力だ!今回その極限値を論理的に求める時が来たのだ!
さて、改めて等式の左辺を見てどうすればよいか考えてみて欲しい。

$$\lim_{h \to 0}\frac{\sin h}{h}$$
はもうこれ以上変形はできない気がするのですが・・・
一体どうするのでしょうか?
『はさみ打ち』が鍵


うむその直感は正しい。こういう時の一つの方法として『はさみ打ち』という技があるのだ。詳しくは下の図を見てくれ。
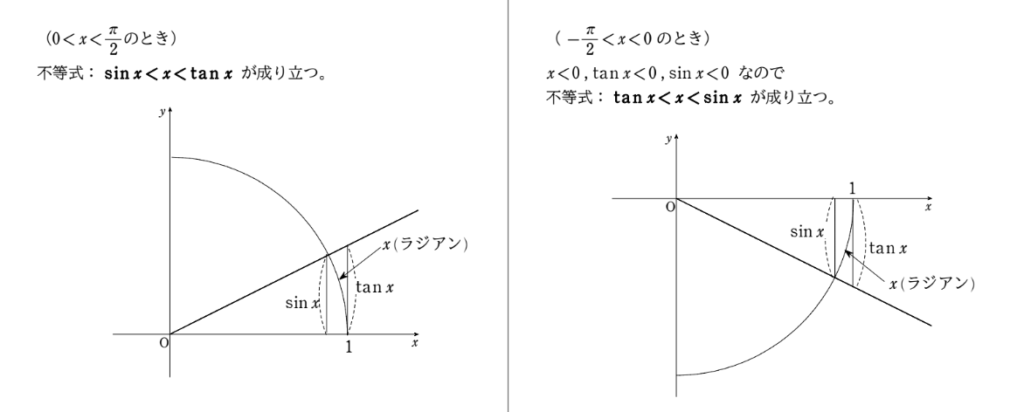

図から分かることはラジアンと \(\sin x\ ,\ \tan x\) の定義から、次の不等式が成り立つということだ。
$$0<x<\frac{\pi}{2} のとき、\sin x<x<\tan x\ \cdots\ ①$$
$$-\frac{\pi}{2}<x<0 のとき、\tan x<x<\sin x\ \cdots\ ②$$

うーん、確かに定義から成り立ちそうだとは思うのですが、図形を用いているのでなんか直感的な感じがします。これはいいのでしょうか?

素晴らしい指摘だ!正にその通りなのだ。図形を用いると視覚的にとても解りやすくなるのだがその分、厳密さが薄くなる。そういうものなのだ。しかし、今学んでいる微分法の考えを応用して上の不等式を厳密に示すことができるようになる。それはもう少し後のことだからそれまではいくぶん直感的な説明で我慢してくれ!図形的な理解もこれはこれで大切なのだ。

そうなのですね!分かりました。今は図形的に理解しておきます。

さて、①と②からいかにして目標である式
$$\frac{\sin x}{x}$$
をはさみ込むかということを考えるのだ。ちょっと難しいからヒントを与えよう。\(\tan x\) を変形するのだ。

$$\tan x=\frac{\sin x}{cos x}$$
という変形ができるから・・・
①について、
$$0<x<\frac{\pi}{2} のとき、\sin x<x<\frac{\sin x}{\cos x}\ \cdots\ (ア)$$
分母の \(\cos x\) 払って
$$\sin x\cos x<x\cos x<\sin x\ \cdots\ (イ)を得る。$$
$$(ア)と(イ)から \sin xに注目すると、x\cos x<\sin x<x\ を得る。$$
両辺 \(x\ (>0)\) で割って、
$$\cos x<\frac{\sin x}{x}<1\ を得る。$$

目標である式
$$\frac{\sin x}{x}$$
をうまくはさむことができたようだな!さあ、後は \(\lim_{x \to 0}\) を発動させるだけだぞ。

はい、続けます。
$$\lim_{x \to 0}\cos x=1\ なので、\lim_{x \to 0}\frac{\sin x}{x}\ は1ではさまれることになる。$$
$$したがって、\lim_{x \to 0}\frac{\sin x}{x}=1\ である。$$

うむ、完璧だ!
②の場合も全く同様にできるから必要があればやってみてくれ。
さて、これで一つ目の極限値については解決したな。もう一つの
$$\lim_{h \to 0}\frac{\cos h-1}{h}$$
がまだ残っているな。これは今、示した公式を用いて計算することができるぞ!これも難しいからヒントをあたえよう!\(\cos h\) についての式から \(\sin h\) を生み出すために分母分子に \(\cos h+1\) をかけるのだ。
$$\lim_{h \to 0}\frac{\cos h-1}{h}\ について$$

それはなかなか気づきませんね!
では、やってみます。
$$\lim_{h \to 0}\frac{\cos h-1}{h}\ の分母分子に\ \cos h+1\ をかけて、$$
$$=\lim_{h \to 0}\frac{(\cos h-1)(\cos h+1)}{h(\cos h+1)}=\lim_{h \to 0}\frac{\cos ^{2}h-1}{h(\cos h+1)}$$
$$=\lim_{h \to 0}\frac{-\sin ^{2}h}{h(\cos h+1)}=-\lim_{h \to 0}\frac{\sin h}{h}\cdot\lim_{h \to 0}\frac{\sin h}{\cos h+1}$$
$$\lim_{h \to 0}\frac{\sin h}{h}\ となることは既に示したので$$
$$=-1 \cdot \frac{0}{1+1}=0$$

結局 \(0\) になるということですか?

ああ、そういうことだ。よくできたな!
長かったがこれでようやく \(\sin x\) の微分が計算できるぞ。
では仕上げをしてくれ!

はい!
$$(\sin x)’= \lim_{h \to 0}\frac{\sin (x+h)-\sin x}{h}=\lim_{h \to 0}\frac{(\sin x\cos h+\sin h\cos x)-\sin x}{h}$$
$$=\lim_{h \to 0}\frac{\sin x(\cos h-1)+\sin h\cos x}{h}$$
$$ここで、\lim_{h \to 0} を分配して、$$
$$=\lim_{h \to 0}\frac{\sin x(\cos h-1)}{h}+\lim_{h \to 0}\frac{\sin h\cos x}{h}$$
$$x だけの関数は \lim_{h \to 0} の影響を受けないので \lim_{h \to 0} の外に出して、$$
$$=\sin x\cdot\lim_{h \to 0}\frac{\cos h-1}{h}+\cos x\cdot\lim_{h \to 0}\frac{\sin h}{h}$$
ここで、
$$\lim_{h \to 0}\frac{\cos h-1}{h}=0\ ,\ \lim_{h \to 0}\frac{\sin h}{h}=1$$
となるので、結局
$$\sin x\cdot\lim_{h \to 0}\frac{\cos h-1}{h}+\cos x\cdot\lim_{h \to 0}\frac{\sin h}{h}=\sin x \cdot 0+\cos x \cdot 1=\cos x$$
となる。したがって、
$$(\sin x)’=\cos x$$

できました!\(\sin x\) を微分するためには多くの知識が必要だということが分かりました。そして、微分した結果は意外にも \(\cos x\) となったのは不思議な感じがします。本当に奥が深いですね!

ああ、そうだな。加法定理や難しい極限値を用いなくては求めることは叶わなかったのだ。そのような複雑な計算の果てに待っていたのは単純な結果 \(\cos x\) であることは確かに不思議な気持ちになるな。さて、今回は多くのことが出てきたからここまでにしよう。ぜひ、読み返してしっかり理解してほしい。次回は他の最重要な関数を微分していくぞ!では今日もお疲れさん。

はい、ありがとうございました!







コメント