はじめに
『二等辺三角形の底角は等しい』・・・この定理はおそらく小学生でも知っている有名なものである。そして中学生ならばきっと、この定理の証明をできるだろう。
このことを踏まえて改めて問おう。
「二等辺三角形の底角は等しいですか?」と。
この質問は、あいまいさや直感を排除した理解がいかに大切かを我々に教えてくれる質問である。
この質問に対して、おそらく多くの生徒は、\(AB=AC\)の二等辺三角形において、\(\angle A\)の二等分線を引くことや、\(辺BC\)の中点を取ることを考えるだろう。
何はともあれ証明してみよう
まずは、証明をしてみよう! 以下に紹介する方法は、教科書にも載っている有名な証明法である。自分でできる人は、ぜひやってみてほしい。
証明1(\(\angle A\) の二等分線を引く方法)
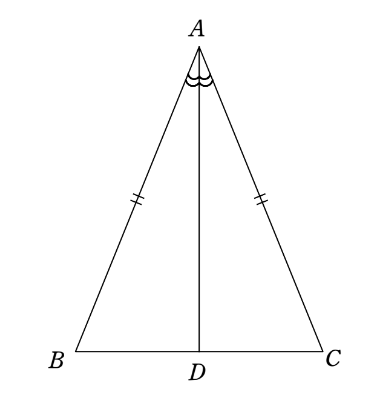
$$\angle Aの二等分線と、辺BCとの交点をDとおく。$$
$$ \triangle ABD と \triangle ACD において、$$
\begin{cases}
AB=AC(仮定)・・・①\\
\angle BAD=\angle CAD・・・②\\
ADは共通・・・③
\end{cases}
$$①~③から\triangle ABD \equiv \triangle ACD(2辺夾角相等)$$
証明2(\(辺BC\) の中点をとる方法)
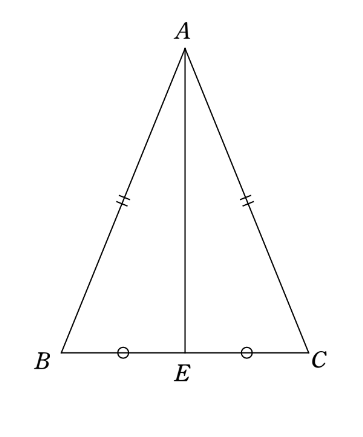
$$辺BCの中点Eとおく。$$
$$ \triangle ABE と \triangle ACE において、$$
\begin{cases}
AB=AC(仮定)・・・①\\
BE=CE・・・②\\
AEは共通・・・③
\end{cases}
$$①~③から\triangle ABE \equiv \triangle ACE(3辺相等)$$
さて、いかがだっただろうか?
とてもシンプルで分かりやすい証明だっただろう。
多くの人が、「ああ、なるほどね!」と思ったのではないだろうか?
とても良い復習になったことだろう? 良かった良かった😊
しかし、しかし、しかし!
正確に言うと、上の二つの証明は場合によっては、どちらも重大な論理的欠陥を孕んでいるのである。
いったいどういう事であろうか? このことをこれから一緒に考えて行こう。
証明の中に潜む循環論法
実は、人によっては、証明1と証明2は共に循環論法に陥っているのだ。
循環論法とは、『証明すべきことを使って証明をすることである』これはもちろん論理的にやってはいけない。例えるなら、自分のつま先をもって自分を持ち上げようとするようなもので、数学の証明としては完全にアウトなのである。
私自身はどうかというと、もちろん陥っていた側の人間だ!
証明1の検証
証明1は \(\angle A\) の二等分線を引く方法であった。ここでちょっと立ち止まって考えてほしいことがある。
それは、『そもそも角の二等分線はどうやって引くのか?』ということである。
作図法を思い出そう。与えられた角を二等分するには次のような方法があった。
(角の二等分線の作図)
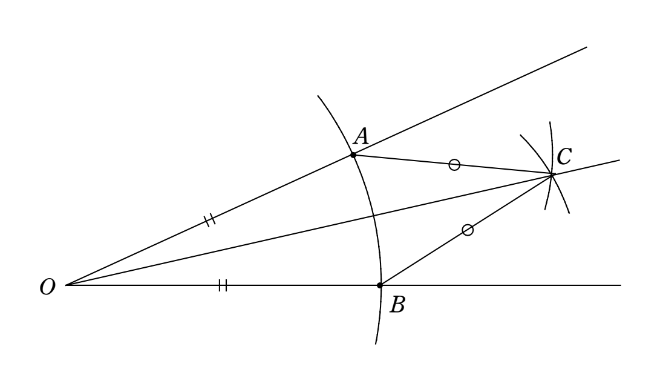
① 右図のように、点 \(O\) を中心としてコンパスで円を描き、角を挟む辺との交点を \(A\)、\(B\)とする。
② 次に、\(A\)、\(B\) を中心として等しい半径の円を描き、それらの交点を \(C\) とすると、線分\(OC\) が求める角の二等分線となる。
では、重要な質問をしよう。
『この作図法を正当化している根拠はなにか?』
つまり、この作図法で \(\angle A\) が二等分されるのはなぜか?という意味だ。
これは次のように説明できる。
角の二等分線の根拠

右図を用いて説明する。
$$ \triangle OAC と \triangle OBC において、$$
\begin{cases}
OA=OB(仮定)・・・①\\
AC=BC(仮定)・・・②\\
OCは共通・・・③
\end{cases}
\(①~③より、\triangle OAC \equiv \triangle OBC\)(三辺相等)
なるほど、角の二等分線の根拠になっていたのは三角形の合同条件の一つである『三辺相等』であったことが分かった。
証明1の検証はいったんここまでにして、今度は証明2の方を検証してみよう。
証明2の検証
証明2は \(辺BC\)の中点をとる方法であった。ここでまた、ちょっと考えてほしいことがある。
それは、『そもそも辺の中点はどうやってとるのか?』ということである。
作図法を思い出そう。与えられた辺の中点を作図するには次のような方法があった。
(垂直二等分線の作図)
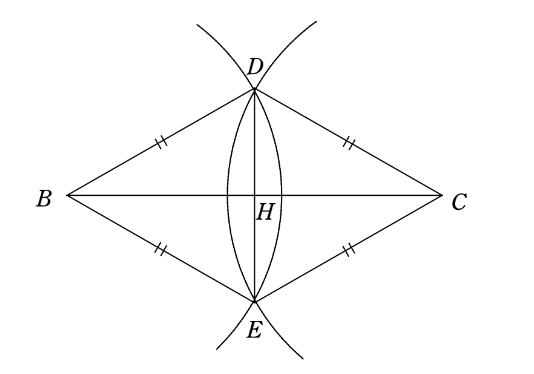
① 右図のように、辺 \(BC\) の端点 \(B\)、\(C\) を中心としてコンパスで等しい半径の円を二つ描き、二つの円の交点を \(D\)、\(E\) とする。
② 線分 \(DE\) と線分 \(BC\) の交点を \(H\) とすると、\(H\) が求める辺\(BC\) の中点となる。
※線分 \(DE\) は線分 \(BC\) の垂直二等分線となる。
これは、線分 \(BC\) の中点の作図というより、線分 \(BC\) の垂直二等分線の作図である。
では、重要な質問をしよう。
『この作図法を正当化している根拠はなにか?』
つまり、この作図法で \(BC\) の垂直二等分線が引けるのはなぜか?という意味だ。
上と同じようにこれは次のように説明できる。
線分の垂直二等分線の根拠

右図を用いて説明する。
目標は \(\triangle BDH \equiv \triangle CDH\) を示すことである。
これが示されれば、\(BH=CH\) かつ \(\angle DHB=\angle DHC\) がいえて、線分 \(DE\) は線分 \(BC\) の垂直二等分線であることがいえる。
\(BD=CD\) かつ \(DH\) は共通なので、\(\triangle BDH \equiv \triangle CDH\) を示すには、あとは \(\angle BDH=\angle CDH\) が欲しい。
(そうすると、二辺夾角相等により、\(\triangle BDH \equiv \triangle CDH\) がいえる。)
結局、\(\angle BDH=\angle CDH\) を示せばよいことが分かった。
これは、次のように証明される。

$$ \triangle BDE と \triangle CDE において、$$
\begin{cases}
BD=CD(仮定)・・・①\\
BE=CE(仮定)・・・②\\
DEは共通・・・③
\end{cases}
\(①~③から\triangle BDE \equiv \triangle CDE\)(三辺相等)
なるほど、線分の垂直二等分線の根拠になっていたのも上と同様に、三角形の合同条件の一つである『三辺相等』であったことが分かった。
証明1と証明2が拠り所としているもの
さて、ここまで検証してきて分かったことがある。すこしまとめてみよう!
合同条件:三辺相等
『二等辺三角形の底角が等しい』という主張の証明として、証明1(角の二等分線を用いる方法)と証明2(線分の垂直二等分線を用いる方法)を挙げたが、これらは結局『三辺相等』という三角形の合同条件を拠り所にしていたのだ。
さあ、ゴールは間近となってきたぞ。ここで最後の重要な質問をしたいと思う。
『合同条件の三辺相等を正当化している根拠は何か』つまり、
『なぜ三辺がそれぞれ等しい三角形は合同になるのか?』と聞いているのだ。
「ん?ちょっと待ってくれ、三辺相等は『合同条件』ではなかったのか?」
「合同条件は証明する必要ないのでは?」
「そもそも三辺が等しければ合同に決まってるじゃないか!一体何を証明しろというんだ? 待て、頭が混乱してきたぞ!」
という心の声が聞こえてきそうである。しかし、当たり前に思えることでもしっかりと証明しなければならない時もある。当たり前と思えることの証明の中に実は本質が隠れているものなのだ。
とにかく紙と鉛筆を出して少しの時間、証明を試みてほしい。
我々は、証明1と証明2が、なぜ循環論法になるのかを考えてきた。その答えは、この最後の質問の証明のなかで得られるだろう。
では、質問の解答に移ろう。
三辺相等を正当化している根拠
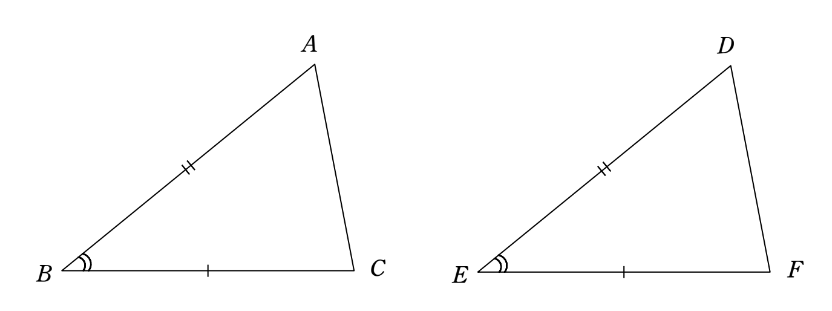
\(\triangle ABC\) と \(\triangle DEF\) は、\(AB=DE、BC=EF、CA=FD\) を満たしているとする。(右図)
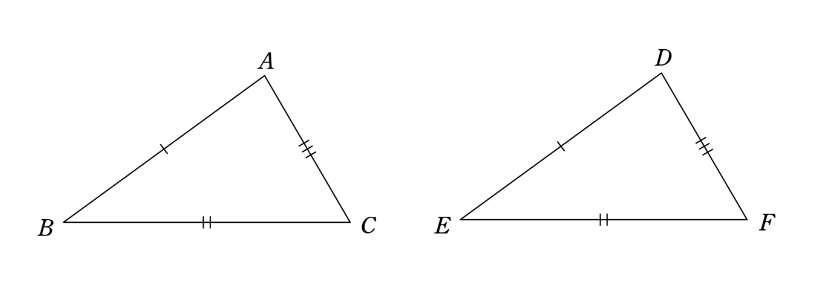
目標は、\(\triangle ABC \equiv \triangle DEF\) であることを、『三辺相等』によらず示したいのだ。つまり、『2辺夾角相等』か『2角夾辺相等』を用いて示さなくてはならない。(これら二つの合同条件については本記事の最後に話をする。)
これはちょっと考えてみると分かるが、なかなか難しくかなりの試行錯誤を要する。
そして、最終的につぎの方法に落ち着くことになる。
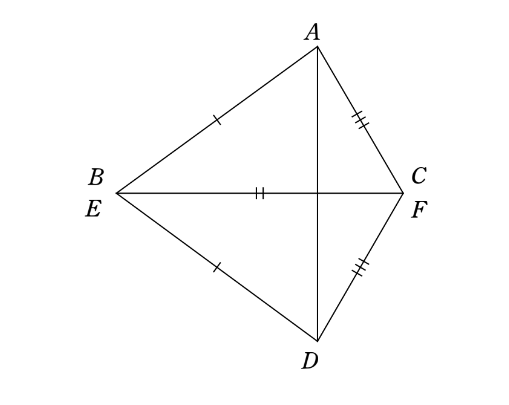
\(\triangle ABC\) と \(\triangle DEF\) を右図のように
上下にくっつけて、線分 \(AD\) を引く。
すると、\(\triangle BAD\) と \(\triangle CAD\) は二等辺三角形なので、\(\angle BAD= \angle BDA\) かつ \(\angle CAD= \angle CDA\) がいえる。等しい二つの角を足しても等しいので、\(\angle A= \angle D\) となるから、\(\triangle ABC\) と \(\triangle DEF\) は合同条件の2辺夾角相等を満たし、\(\triangle ABC \equiv \triangle DEF\) が示される。
気づいただろうか?
そう、三辺相等を正当化するには、『二等辺三角形の底角が等しい』ことを用いなければならないのだ! いやいや、二等辺三角形を使わない証明法を探せばいいではないか!と思うだろう?もちろん私もそう考えて、いろいろ試してみたがどう頑張っても二等辺三角形を使わざるを得ないのだ!
ところが、『二等辺三角形の底角が等しい』ことを証明するのが本来の目的であった。
これは、循環論法である。
まとめ
さて、だいぶ長くなったのでここで、ここまでの話をまとめてみよう。
我々の最初の目的は『二等辺三角形の底角は等しい』ことを証明することであった。
そこで、二つの証明法を提示した(これらは、教科書にも載っている方法である)。それらは、
\begin{cases}
① 証明1:角の二等分線を用いる方法\\
② 証明2:線分の垂直二等分線を用いる方法
\end{cases}であった。
これらの証明法は、どちらも合同条件の『三辺相等』を根拠の拠り所としていた。
しかし、『三辺相等』は『二等辺三角形の底角が等しい』ことを根拠の拠り所としていた。
『二等辺三角形の底角が等しい』は証明すべきことなので、これは循環論法となってしまう。
なので、証明1と証明2は『二等辺三角形の底角が等しい』ことの証明にはならないということだ。
では、どうやって『二等辺三角形の底角が等しい』ことを証明するのだろう? 安心してほしい、三辺相等によらない方法がちゃんとあるのだ!
真の証明
ユークリッド原論で有名な数学者ユークリッドは、上で紹介した循環論法にもちろん気づいていたと思われる。その証拠にユークリッドは『二等辺三角形の底角が等しいことの証明』を非常に長く難解な方法で証明したという。(ここでは紹介しないので興味のある人は原論を読んでみるといいだろう。原論は大きめの図書館に大体置いてある)。
ここで紹介するのは、ユークリッドのオリジナルの方法ではなく、ユークリッドより500年ほど後の時代に生まれた『パッポス』の考えた証明である。非常にシンプルで分かりやすい証明である。証明は『二辺夾角相等』に依る方法である。
『二等辺三角形の底角が等しい』ことの真の証明(パッポス)
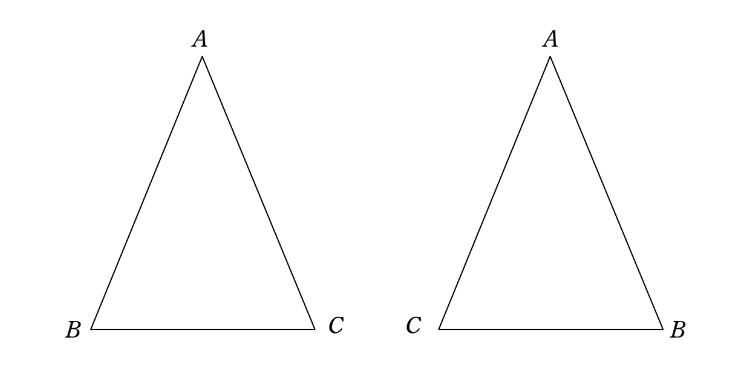
(証明)二等辺三角形 \(ABC\) を裏返して、二等辺三角形 \(ACB\) を考える.
これら二つの三角形について、仮定により、\(AB=AC、AC=AB\) はもちろん成り立っている。また、裏返したので当然 \(\angle A\) は共通で等しい。
したがって、二辺夾角相等により、\( \triangle ABC \equiv \triangle ACB\) がいえる。
対応する角は等しいので、\(\angle B = \angle C\). \(q.e.d.\)
いかがだったであろうか? これが、三辺相等に依らない証明法である。
ユークリッドがなぜこの証明法に気づかなかったのか、想像してみると2000年近く昔の幾何学において、図形をひっくり返すなんて発想は生まれなかったのだろう。むしろ、そんなことはご法度としていた可能性もある。いずれにしても、現代のわれわれにも中々できない発想である。
『二辺夾角相等』と『二角夾辺相等』について
上のように三辺相等は、『二辺夾角相等』によって示された。
ここで、次のように思わないだろうか?
三辺相等が正しいことを証明する必要があるのならば、他の合同条件:『二辺夾角相等』と『二角夾辺相等』が正しいことも証明すべきではないのか?と。
その通りである! あのユークリッドもちゃんと証明しているのだ。
ではどうやって証明するのかというと、それは、『公理』に依って証明するのだ。
公理というのは、すべての議論の出発点となる『約束事』のようなものだと考えてほしい。
例えば、『2点を通る直線は一本しかない』、『平行でない2本の直線は一点で交わる』、『すべての直角は等しい』などがある。
これらは、あまりに当たり前すぎて証明ができない。
『約束事』と表現したのが分かってもらえるのではないだろうか?
ここでは、『二辺夾角相等』が正しいことを公理に従って証明してみよう。
『二辺夾角相等』が正しいことの証明
(証明)
\(\triangle ABC\) と \(\triangle DEF\) は、\(AB=DE、BC=EF、\angle B=\angle E\) を満たしているとする。
仮定より、\(\angle B=\angle E\) なので、これらの角は重ね合わせることができる。
そして仮定より、\(AB=DE、BC=EF\) であるから、角をはさむそれぞれの辺上に、\(A、D\) そして、\(C、F\) を同じ位置に取ることができる。

問題は、これら2点を通る直線は何本引けるかということであるが、公理により、『2点を通る直線は1本だけである』からこれら二つの三角形はぴったり重なる。したがって、二辺夾角相等であるふたつの三角形は合同である。\(q.e.d.\)
いかがだっただろう? 上の証明で、もしも2点を通る直線が二本引けるのであれば、異なる二つの三角形ができてしまい、合同ではなくなる。だから、『2点を通る直線は1本だけである』という公理がどうしても必要なのだ。
『二角夾辺相等』が正しいことの証明も同じように公理を用いてできる。ただし、使う公理は『平行でない二本の直線は一点で交わる』である。
こちらの証明は、ぜひ自分でやってみるとよいだろう。
正しい議論の進め方
これまでの話から、『議論の進め方』に神経を払わなければならないことが分かった。『二等辺三角形の底角が等しい』という定理を証明するには、まず『二辺夾角相等』を正当化してから証明する。
そして、『二等辺三角形の底角が等しい』ことが証明されたならば、これを用いて『三辺相等』は証明される。そうすれば、証明1と証明2は、『二等辺三角形の底角は等しい』という定理の別証明として有効となる。三辺相等が正当化されたならば、『角の二等分線』と『辺の垂直二等分線』は問題なく使えるからだ。
議論の進め方には細心の注意を払いたいものである。何が使えて、何がまだ使えないのかを明確にして議論を進めることが大切だ。
最後に
今回、『二等辺三角形の底角は等しい』ことの証明に潜む循環論法について詳しく見てきた。
核心を一言でいうと、それは、『三辺相等』を正当化するためには『二等辺三角形の底角は等しい』ことを使わなければならない、ということであった。
ここで、しっかり伝えておきたいことは、
『三辺相等』を正当化するための方法は、本当に『二等辺三角形の底角は等しい』ことを使う以外ないのか?
という疑問である。これは、正直確信が持てないのだ。いろいろな手段を試した結果、他に方法がなかったと言っているだけであり、そこには何も数学的な根拠はない。
もしも、『二等辺三角形の底角は等しい』ことを使わずに『三辺相等』が証明できたなら、
今回の証明1、証明2は循環論法ではなくなり、有効な証明となるのだ。
今回この記事で言っていることは、『三辺相等』が正しいことの証明に、『二等辺三角形の底角は等しい』ことを使っている以上は、証明1と証明2は循環論法になってしまうという話であることを強調したい。
よって、三辺相等が正しいことを証明せよと問うたとき、二等辺三角形を利用してしまう人はまず、この循環論法に陥っているだろう。(最初に伝えた通り、私自身がそうであった。)
もし、『二等辺三角形の底角は等しい』ことを使わない『三辺相等』の証明を見出せたなら、その時はぜひ教えてほしい。
ここまで、お付き合いいただきありがとう!
もし気づいたことがあったら気軽にコメントしてほしい。
ではまた!




コメント